「树 Tree」
树是一种非线性数据结构,其是一种「无环连通图」—— 即: 树中的 边数 = 结点数 - 1 .
度为 m 的树和 m 叉树的区别
| 度为 m 的树 | m 叉树 |
|---|
| 任意结点的度 ≤m | 任意结点的度 ≤m |
| 至少有一个结点度 =m | 允许所有结点的度都 <m |
| 一定为非空数,至少有 m+1 个结点 | 可以是空树 |
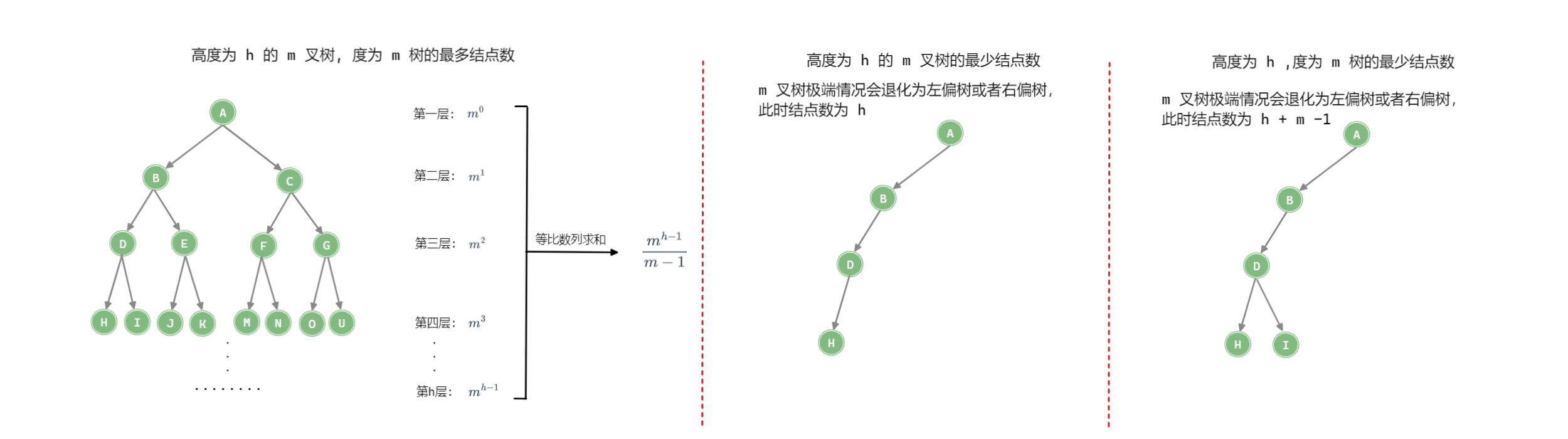
| 度为 m 的树 | m 叉树 |
|---|
| 第 i 层结点数 n | n≤mi−1 | n≤mi−1 |
| 高度为 h 的树的结点数 n | h+m−1≤n≤m−1mh−1 | h≤n≤m−1mh−1 |
| 具有 n 个结点的树的高度 h | | h≥⌈logm(n(m−1)+1)⌉ (最小高度) |
详情
具有 n 个结点的 m 叉树的高度 h 的最小高度推导过程:
m−1mh−1−1<n≤m−1mh−1
mh−1<n(m−1)+1≤mh
h−1<logm(n(m−1)+1)≤h
hmin=⌈logm(n(m−1)+1)⌉
注意
这里的高度 h 是指根结点到最远叶结点之间 “结点” 的数量。
树形数据结构







