二叉树
「二叉树 Binary Tree」
二叉树的定义及主要特征
二叉树是一种特殊的树型结构,其特点有:
- 每个结点至多有两颗子树 ( 即不存在度大于 的结点 )
- 二叉树的子树有左右之分,其次序是不能任意颠倒。( 若将二叉树的左、右子树颠倒,其会变为另一颗二叉树 )
区分二叉树与度为 2 的树
- 二叉树并不是度为 的树,二叉树上的结点的度可以是 。
二叉树常用术语
- 「根结点 Root Node」:二叉树最顶层的结点,其没有父结点;
- 「叶结点 Leaf Node」:没有子结点的结点,其两个指针都指向
null; - 结点所处「层 Level」:从顶置底依次增加,根结点所处层为 ;
- 结点「度 Degree」:结点的子结点数量,二叉树中度的范围是 ;
- 「边 Edge」:连接两个结点的边,即结点指针;
- 二叉树「高度 、深度」:二叉树中根结点到最远叶结点走过边的数量;(根 — 叶)
- 结点「深度 Depth」 :根结点到该结点走过边的数量;(根 — 结点)
- 结点「高度 Height」:最远叶结点到该结点走过边的数量;(结点 — 叶)
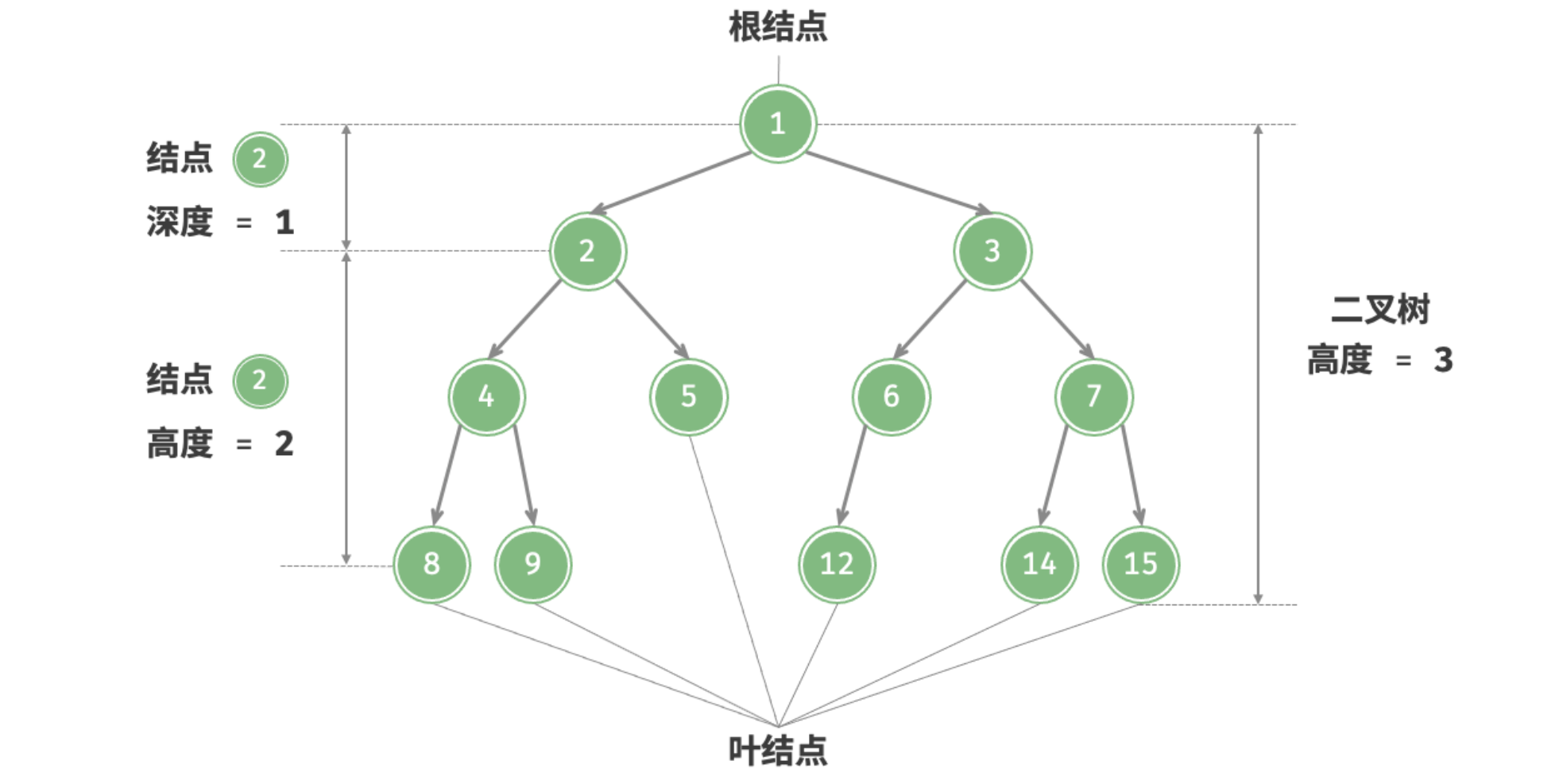
高度和深度的定义
高度和深度的定义并不只有 “边” 的定义,也有以 “结点个数” 定义的,所以当以结点个数作为定义时,需要在以边为标准的基础上 + 1.
常见二叉树
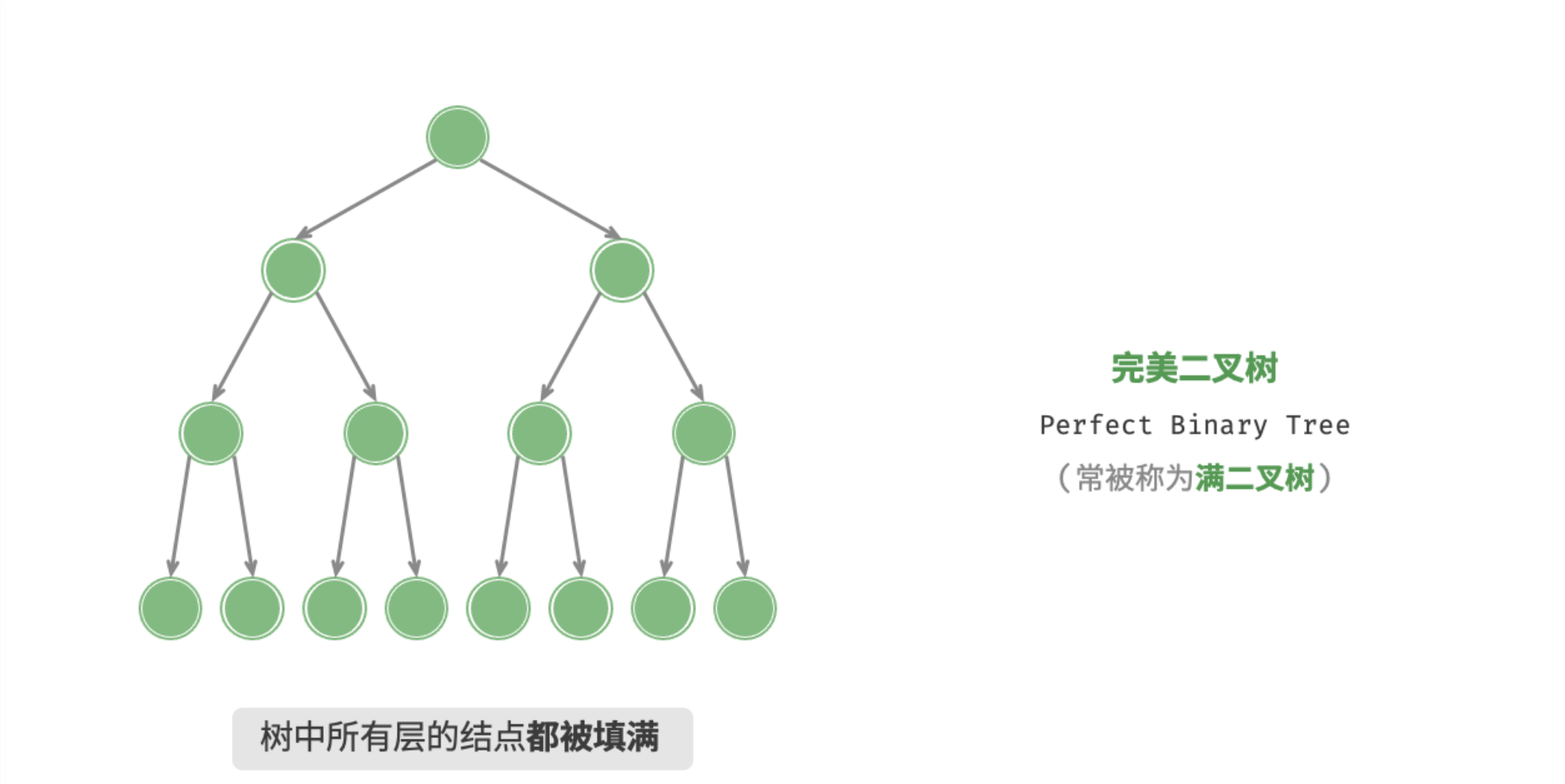
完美二叉树(满二叉树)
「完美二叉树 Perfect Binary Tree」的所有层的结点都被完全填满。在完美二叉树中,所有结点的度 = 2 ;若树高度 = ,则结点总数 = ,呈标准的指数级关系。
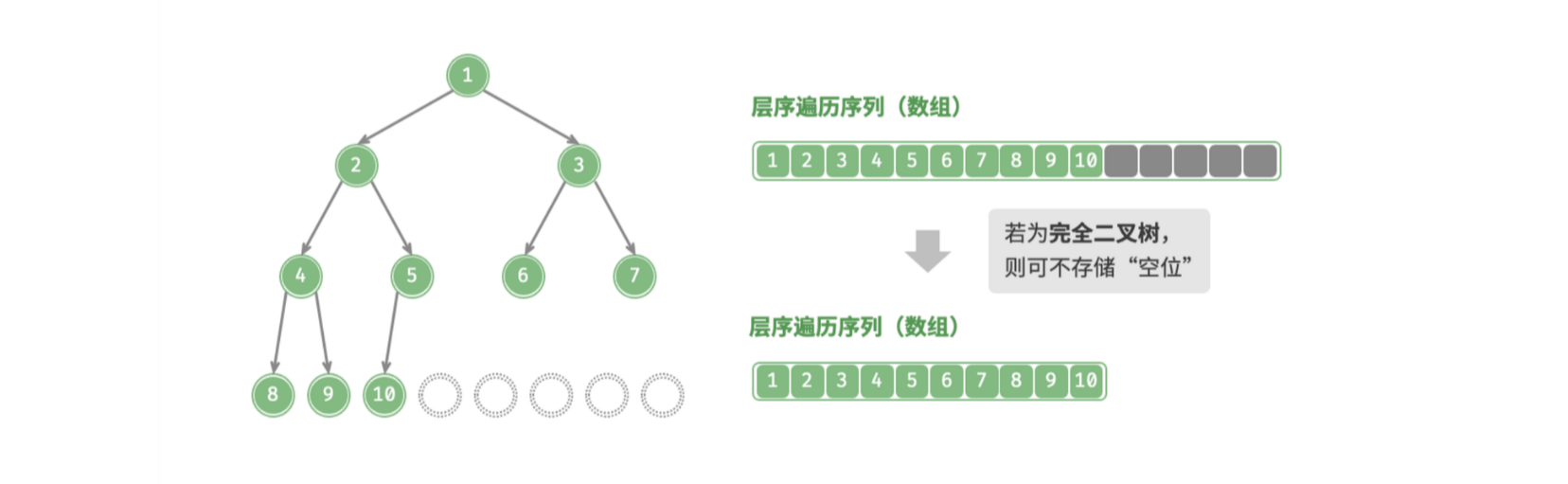
完全二叉树
「完全二叉树 Complete Binary Tree」只有最底层的结点未被填满,且最底层结点尽量靠左填充。
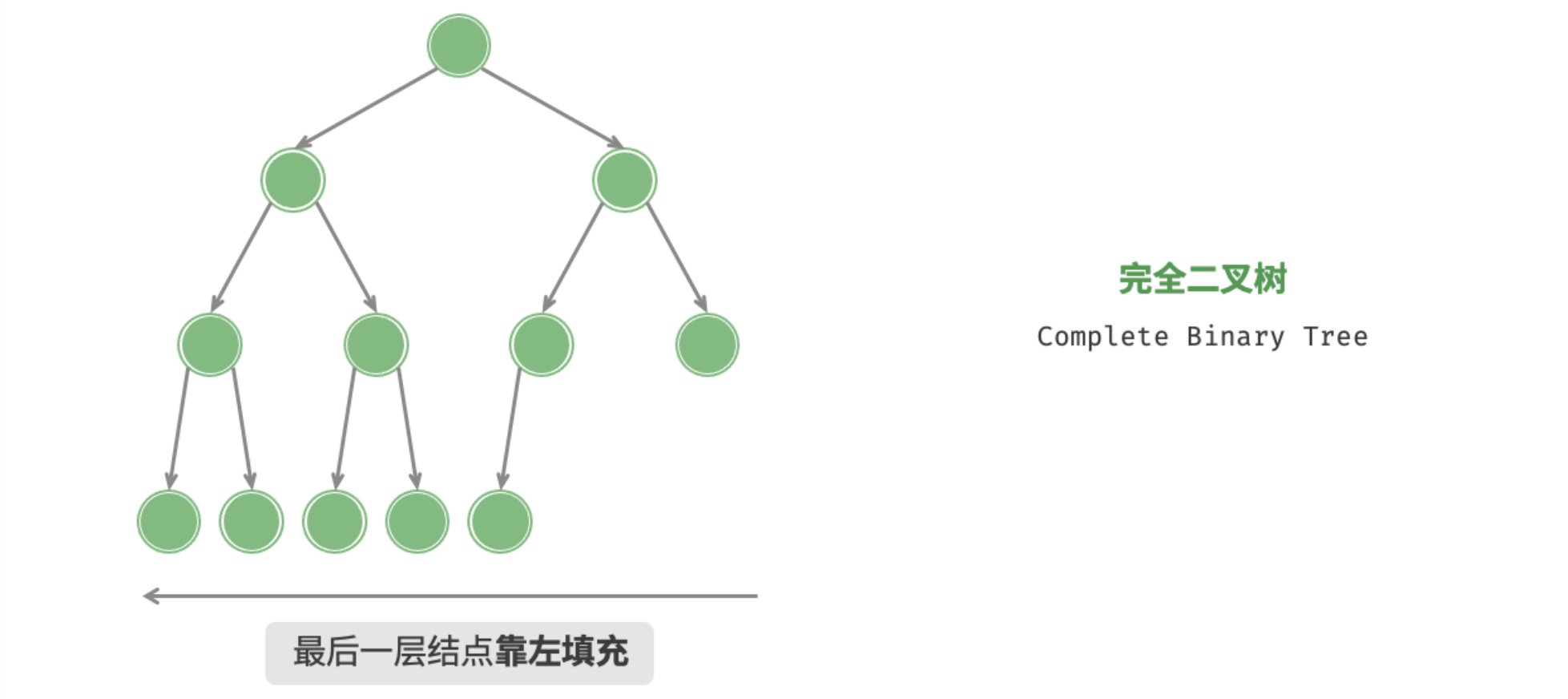
完全二叉树非常适合用数组来表示。如果按照层序遍历序列的顺序来存储,那么空结点 null 一定全部出现在序列的尾部,因此我们就可以不用存储这些 null 了。
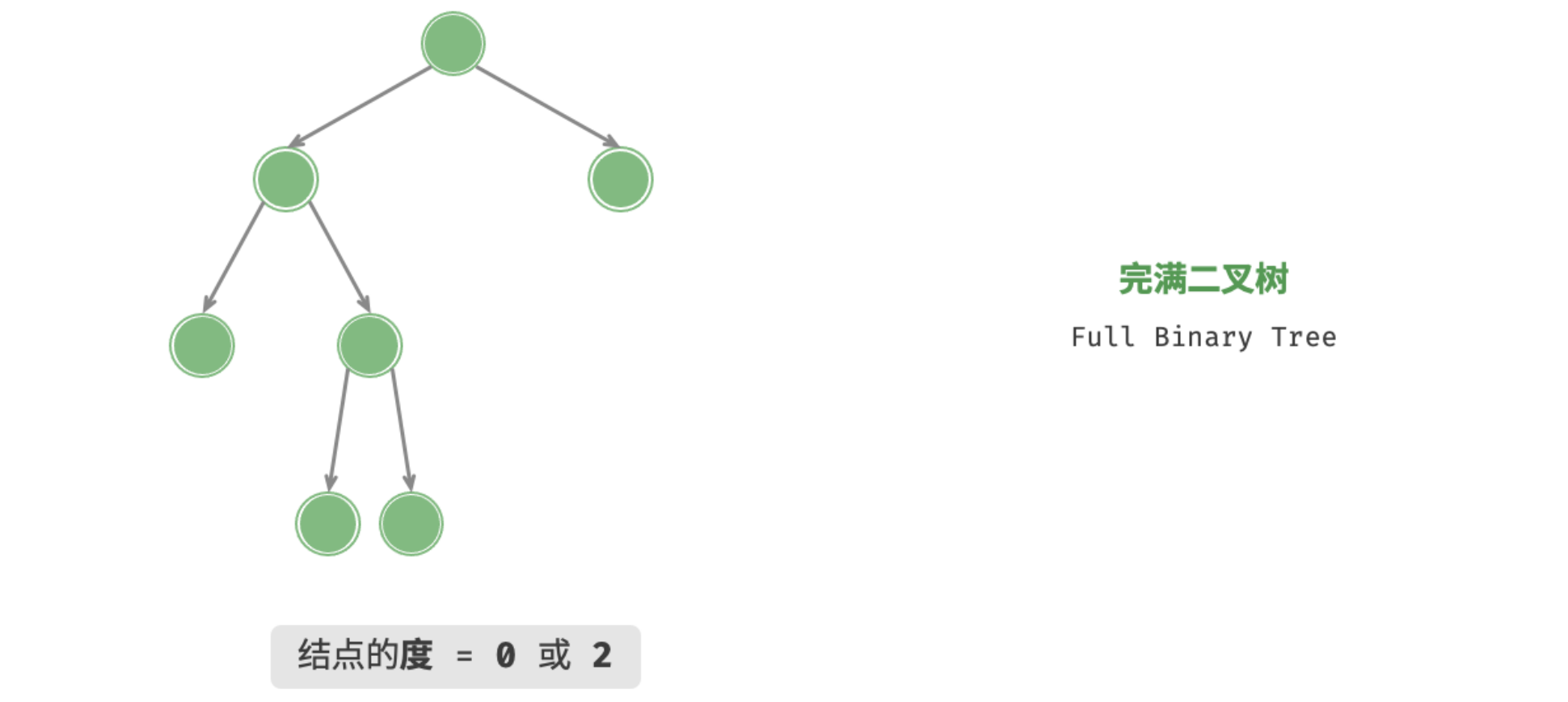
完满二叉树
「完满二叉树 Full Binary Tree」除了叶结点之外,其余所有结点都有两个子结点。
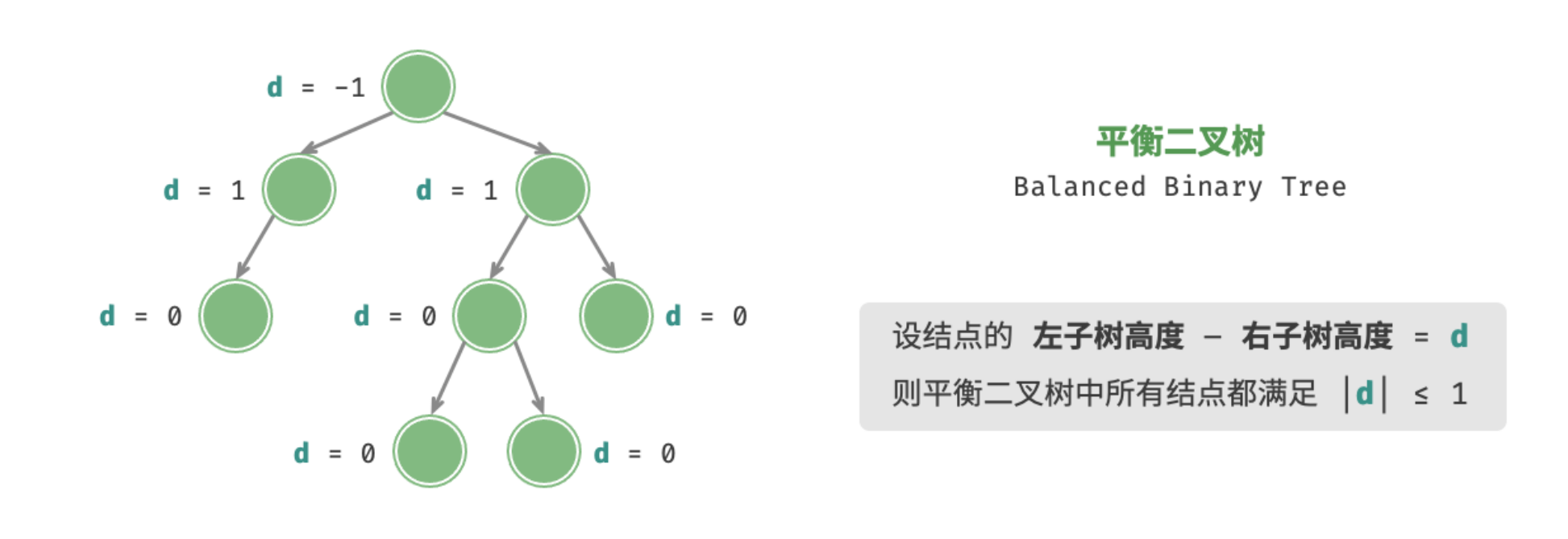
平衡二叉树
「平衡二叉树 Balanced Binary Tree」中任意结点的左子树和右子树的高度之差的绝对值 。
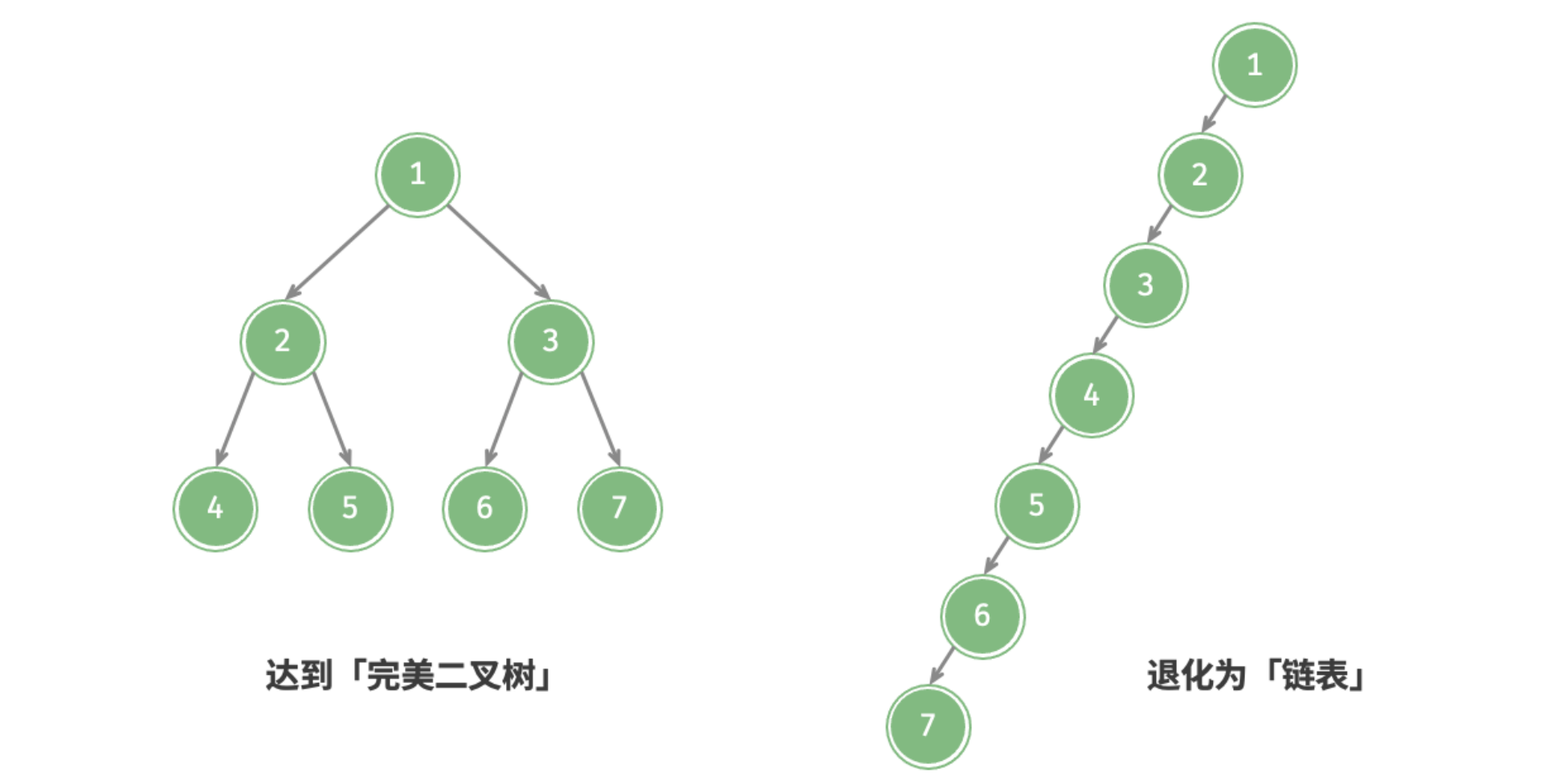
二叉树的退化
当二叉树的每层的结点都被填满时,达到「完美二叉树」;而当所有结点都偏向一边时,二叉树退化为「链表」。
- 完美二叉树是一个二叉树的“最佳状态”,可以完全发挥出二叉树“分治”的优势;
- 链表则是另一个极端,各项操作都变为线性操作,时间复杂度退化至 ;
完美二叉树和退化为链表的二叉树的叶结点数量、结点总数、高度等达到极大或极小值。
| 完美二叉树 | 链表 | |
|---|---|---|
| 第 层结点数量 | ||
| 树的高度为 时叶结点的数量 | ||
| 树的高度为 时结点的数量 | ||
| 树的结点总数为 时的深度 |
二叉树的基本特征
二叉树也是树,而树是 无环连通图 ,所以有 个结点的树,其边的数量 .
- 非空二叉树上的叶子结点数等于度为 的结点数加 ,即 .
- 对一颗具有 个结点的完全二叉树中的结点从 开始按层序编号,则对于任意的编号为 的结点有:
- 如果 ,则结点 的双亲的编号为 ;否则结点 为根结点.
- 如果 ,则结点 的左孩子的编号为 ,否则结点 无左孩子.
- 如果 ,则结点 的右孩子的编号为 ,否则结点 无右孩子.
- 结点所在的深度为 .
对性质的推导
- 性质 1 的证明:
一颗二叉树的结点总数 ,边的总数 ,所以得: . 即:.
二叉树的表示方式
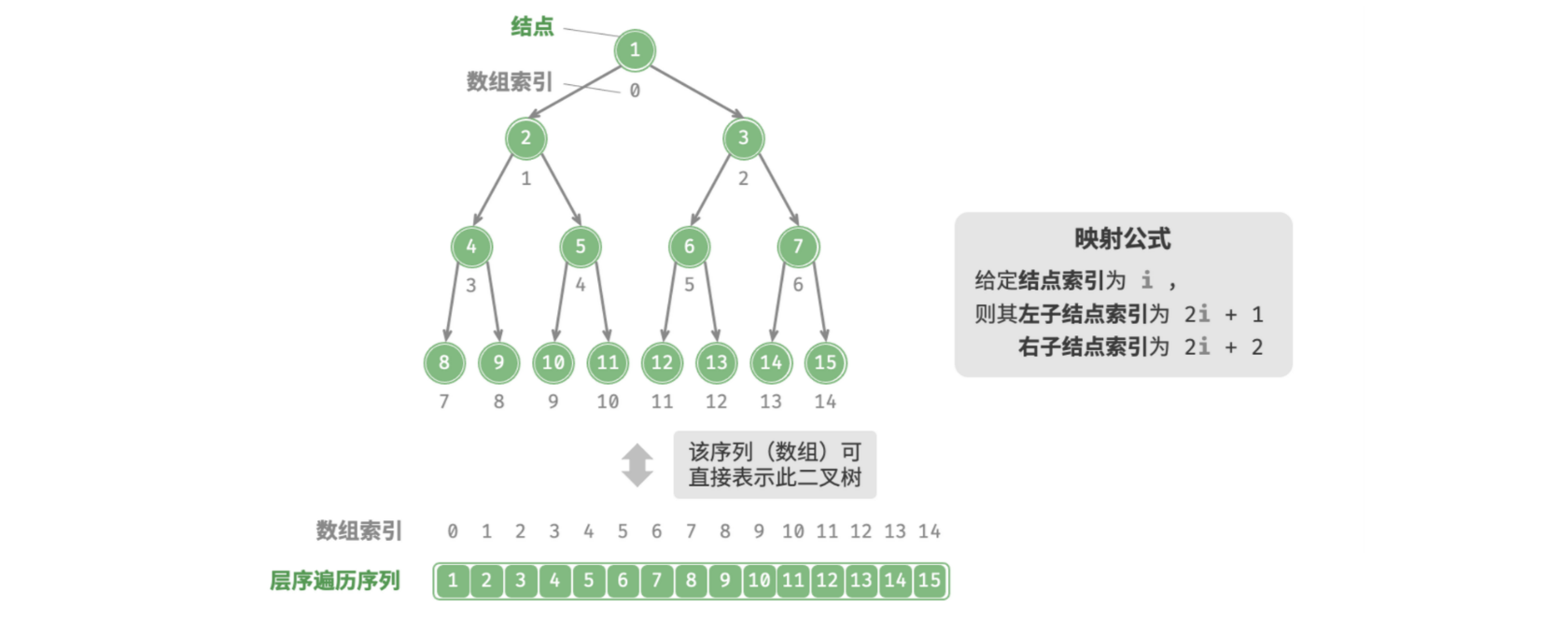
1.数组表示
使用普通数组存储二叉树时,不能直接在结点中存储结点之间的关系,需要推导父结点索引与子结点索引的「映射公式」:设结点的索引为 ,则该结点的左子结点索引为 、右子结点索引为 。
例如数组存储满二叉树:
但是满二叉树的并不常见,要想使用使用数组存储其他类型的二叉树,就必然存在 null 值,即需要将一颗不是满二叉树的二叉树用空结点填充为一颗满二叉树。如下图:
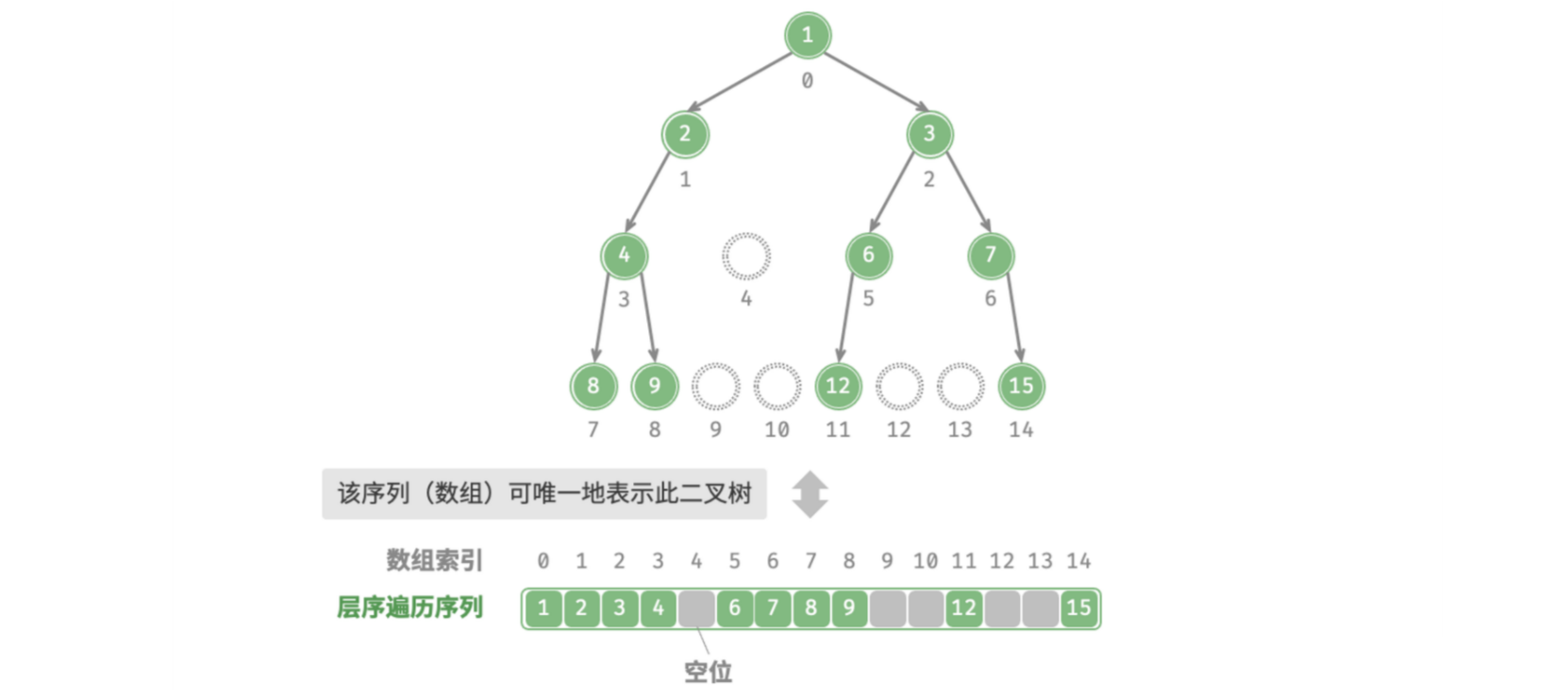
对于完全二叉树来说,其虽然有空结点,但是由于使用层序遍历的顺序存储的原因,这些空结点都在数组的结尾,这使得可以直接不对其进行存储,所以使用数组表示完全二叉树更加合适。
2.链表表示
public class TreeNode<T>{
public T value; // 结点值
public TreeNode<T> left; // 左子结点
public TreeNode<T> right; // 右子结点
public TreeNode(T value) {
this.value = value;
}
}
二叉树的遍历
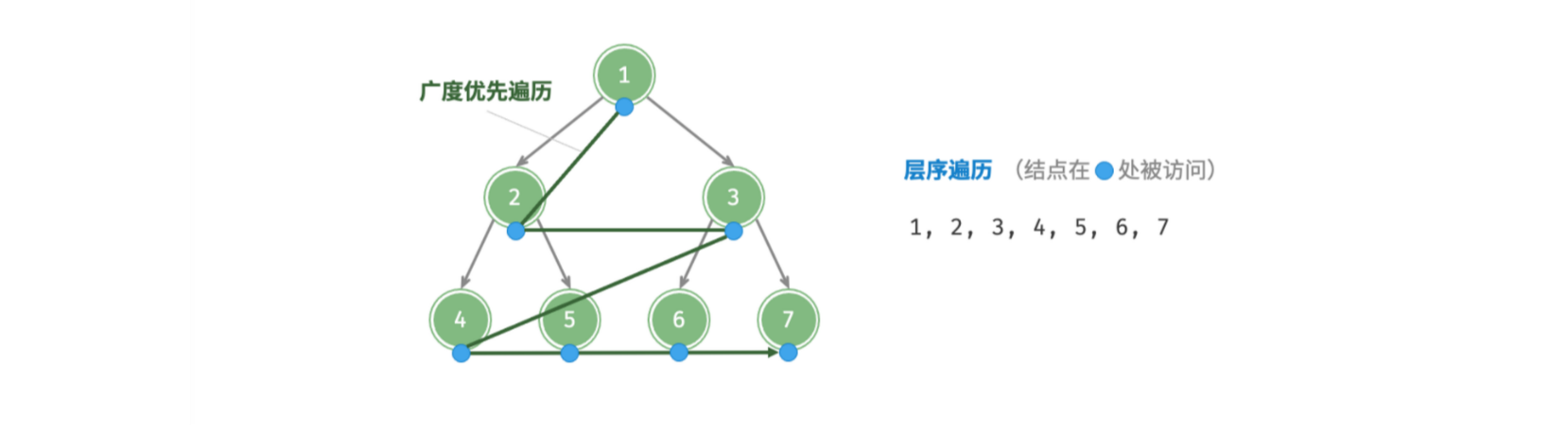
层序遍历
「层序遍历 Hierarchical-Order Traversal」从顶至底、一层一层地遍历二叉树,并在每层中按照从左到右的顺序访问结点。层序遍历本质上是「广度优先遍历 Breadth-First Traversal」.
/**
* 层序遍历
* @param root: 根结点
* @return 层序遍历序列数组
*/
public List<TreeNode<T>> bfsOrder(TreeNode<T> root) {
// 初始化队列, 根结点入队
Queue<TreeNode<T>> queue = new LinkedList<>();
queue.add(root);
// 保存层序遍历的序列
List<TreeNode<T>> list = new ArrayList<>();
while (!queue.isEmpty()) {
TreeNode<T> node = queue.poll(); // 结点出队
list.add(node); // 保存结点(序列)
// 访问左子结点
if(node.left != null) {
queue.offer(node.left);
}
// 访问右子结点
if(node.right != null) {
queue.offer(node.right);
}
}
return list;
}
前序、中序、后序遍历
相对地,前、中、后序遍历皆属于「深度优先遍历 Depth-First Traversal」,即每次搜索会直接搜索到叶子结点,然后再回溯去搜索其他的结点。
如下图所示,左侧是深度优先遍历的的示意图,右上方是对应的递归实现代码。深度优先遍历就像是绕着整个二叉树的外围“走”一圈,走的过程中,在每个结点都会遇到三个位置(即是向下继续搜索左子结点、右子结点或是回溯到父结点),分别对应前序遍历、中序遍历、后序遍历。
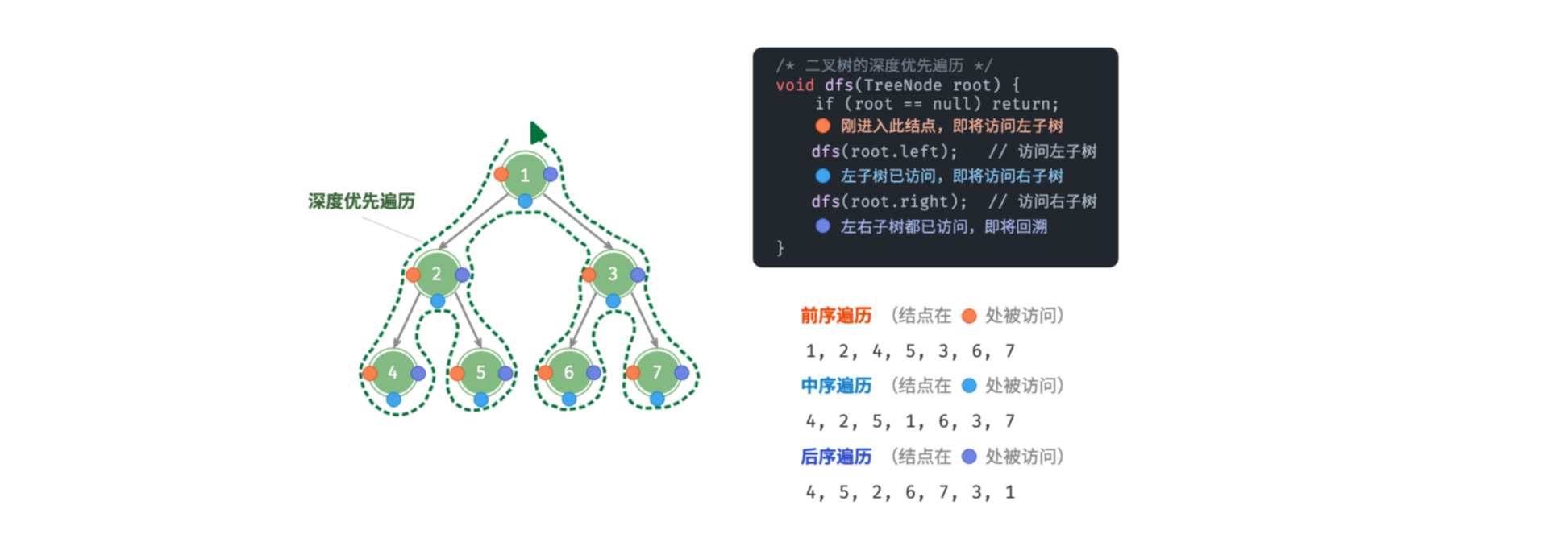
| 位置 | 含义 | 此处访问结点时对应 |
|---|---|---|
| 橙色圆圈处 | 刚进入此结点,即将访问该结点的左子树 | 前序遍历 Pre-Order Traversal |
| 蓝色圆圈处 | 已访问完左子树,即将访问右子树 | 中序遍历 In-Order Traversal |
| 紫色圆圈处 | 已访问完左子树和右子树,即将返回 | 后序遍历 Post-Order Traversal |
由遍历序列确认二叉树
- 前序 / 后序遍历和中序遍历可以唯一确定一颗二叉树
- 前序遍历和后序遍历不能唯一确定一颗二叉树
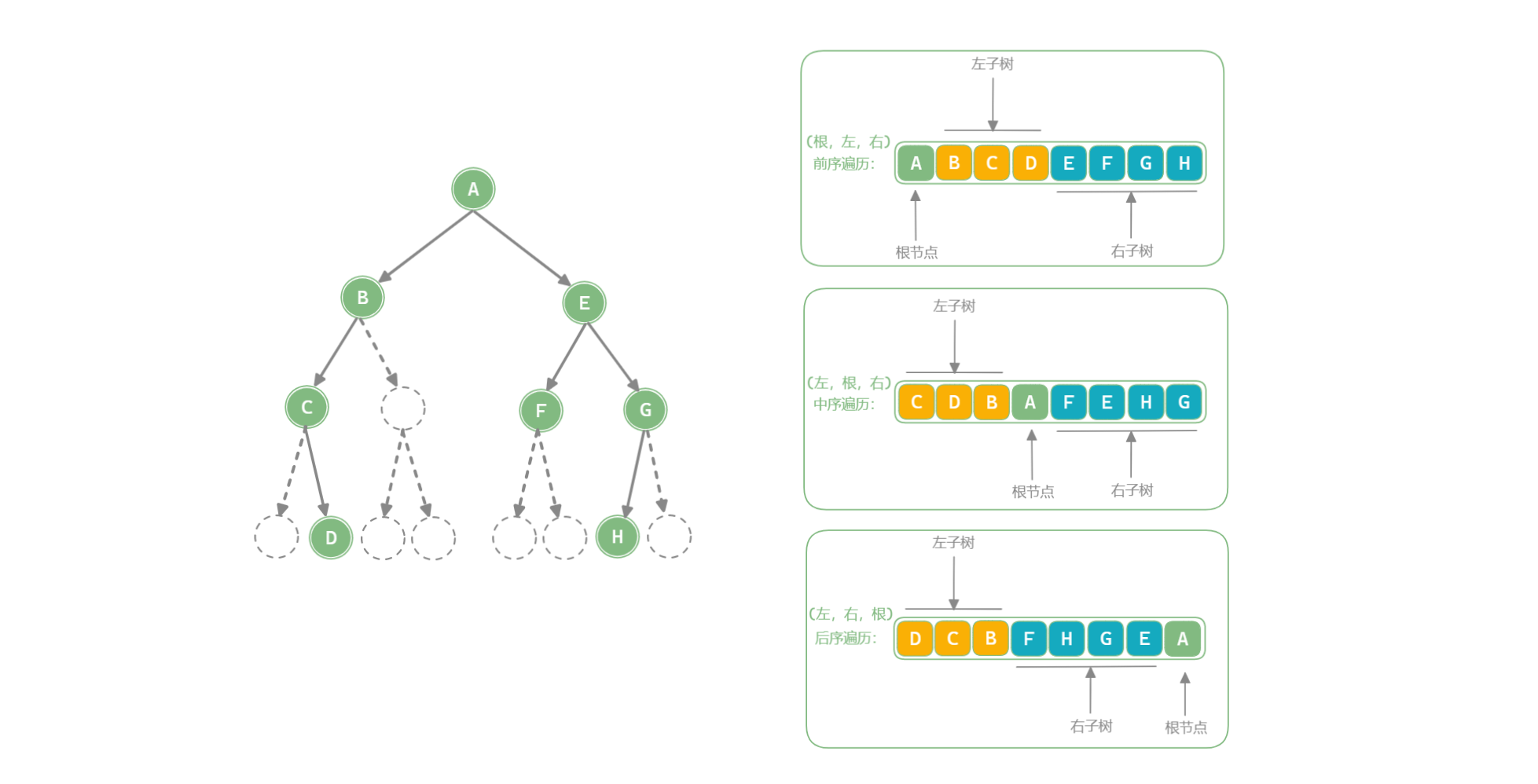
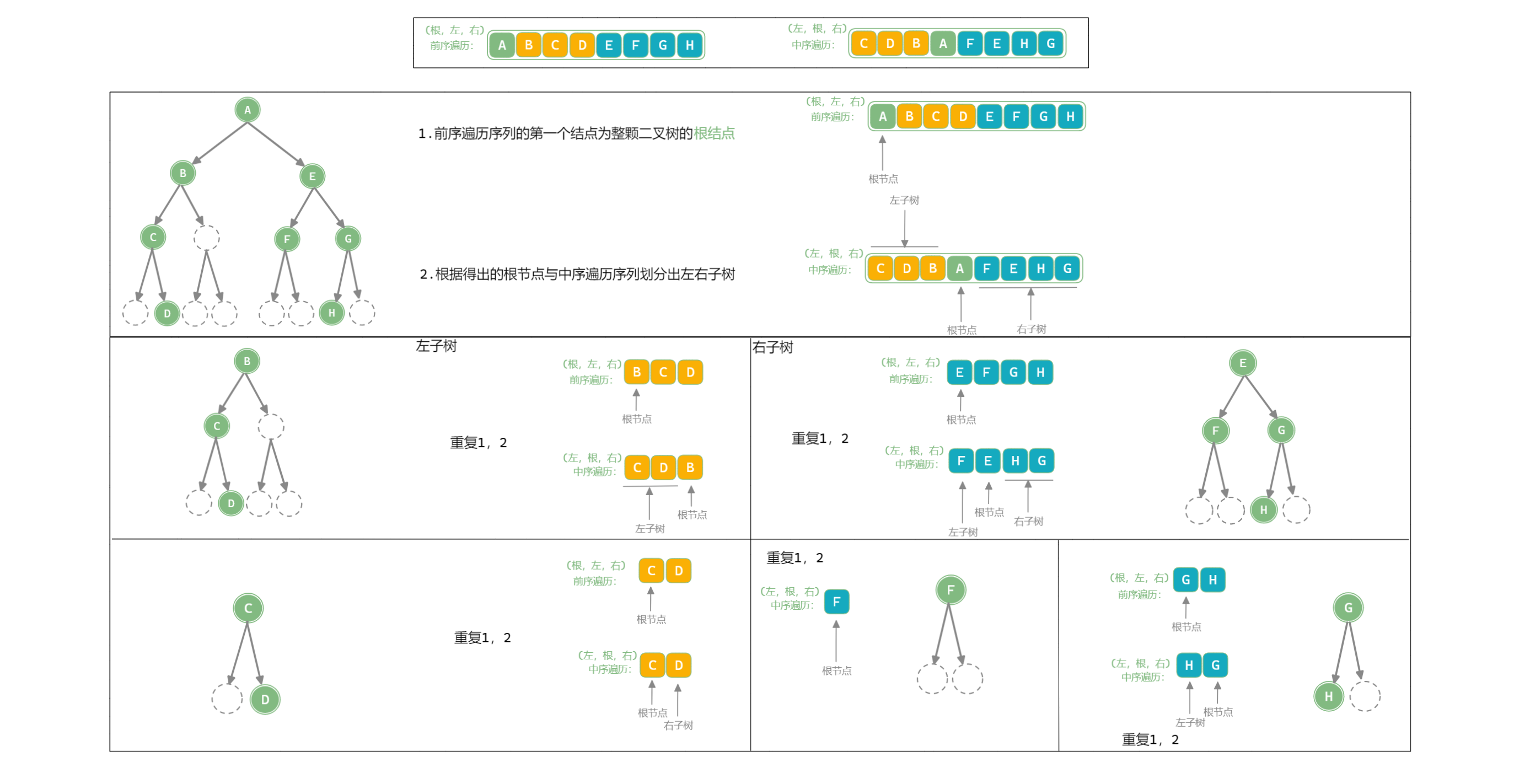
【求解一颗二叉树某一遍历顺序序列】
这三种序列都是从根结点开始的深搜序列,根据其选择的优先级顺序,例如前序遍历为 (根,左,右) (这是根,左,右是相对而言的,不是整颗树的),例如上图中二叉树的前序遍历思考过程如下:
- 首先是到
A(根)结点,是 “根” ,入序列,然后根据(根,左,右)原则遍历该 “根结点” 的 “左” 结点, - 来到左结点
B, 是 “左” ,入序列,因为是深度优先,所以继续根据(根,左,右)原则向下遍历以B为 “根” 的子树,直至以B为 “根” 的子树遍历完毕, - 对于
A(根)结点来说,(根,左)已经遍历完毕,然后继续遍历 “右” ,即来到E,是 “右” ,入序列,然后继续前序遍历原则直接所有结点遍历结束.
【根据前序 / 后序遍历和中序遍历唯一确定一颗二叉树】
/**
* 前序遍历(递归), 序列存储在 list 中
* @param root: 根结点
* @param list: 存储遍历顺序
*/
public void preOrder(TreeNode<T> root, ArrayList<TreeNode<T>> list) {
if (root == null) return;
// 访问优先级: 根结点 -> 左子树 -> 右子树
list.add(root);
preOrder(root.left, list);
preOrder(root.right, list);
}
/**
* 中序遍历(递归), 序列存储在 list 中
* @param root: 根结点
* @param list: 存储遍历顺序
*/
public void inOrder(TreeNode<T> root, ArrayList<TreeNode<T>> list) {
if (root == null) return;
// 访问优先级:左子树 -> 根结点 -> 右子树
inOrder(root.left, list);
list.add(root);
inOrder(root.right, list);
}
/**
* 后序遍历(递归), 序列存储在 list 中
* @param root: 根结点
* @param list: 存储遍历顺序
*/
public void postOrder(TreeNode<T> root, ArrayList<TreeNode<T>> list) {
if (root == null) return;
// 访问优先级:左子树 -> 右子树 -> 根结点
postOrder(root.left, list);
postOrder(root.right, list);
list.add(root);
}
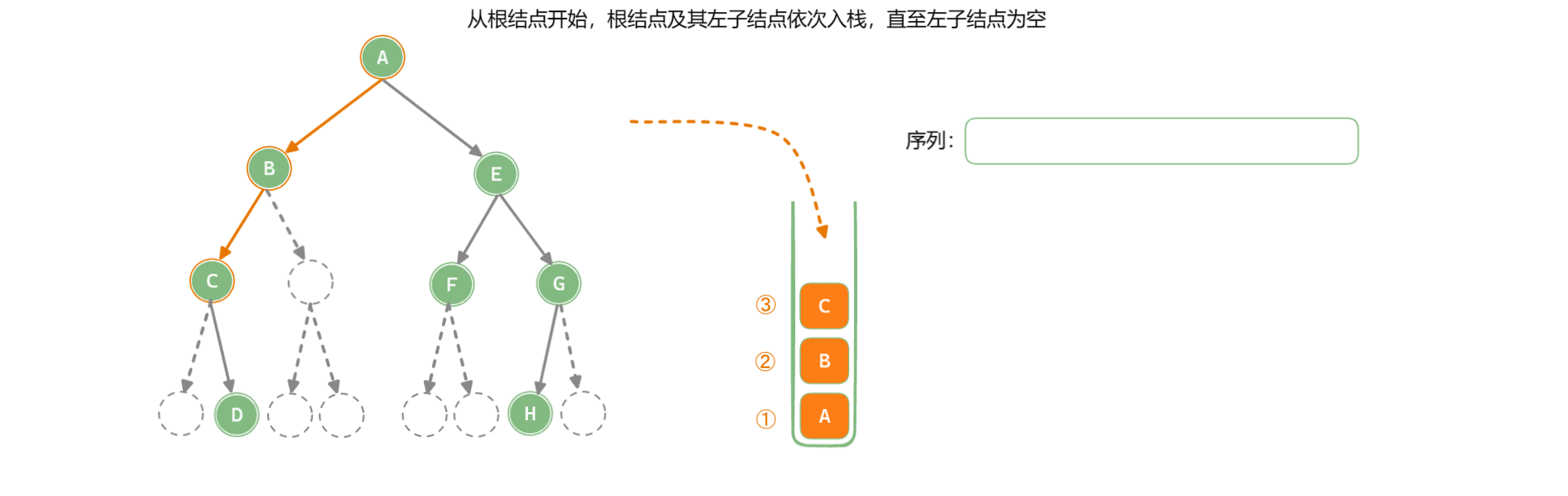
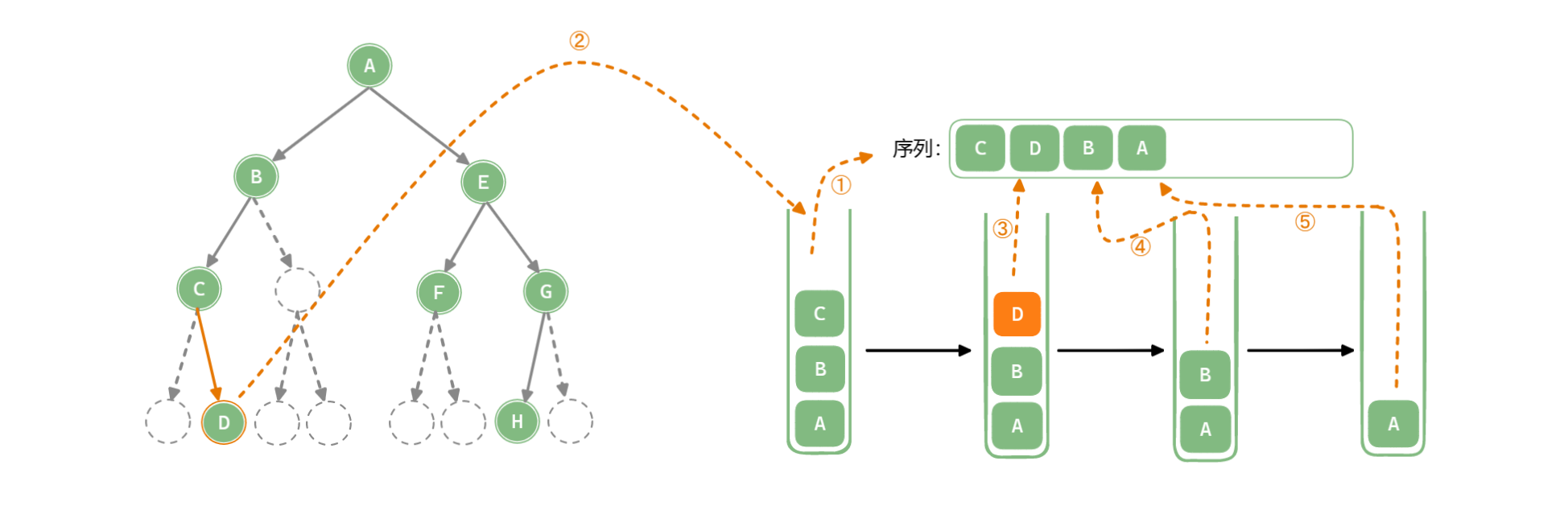
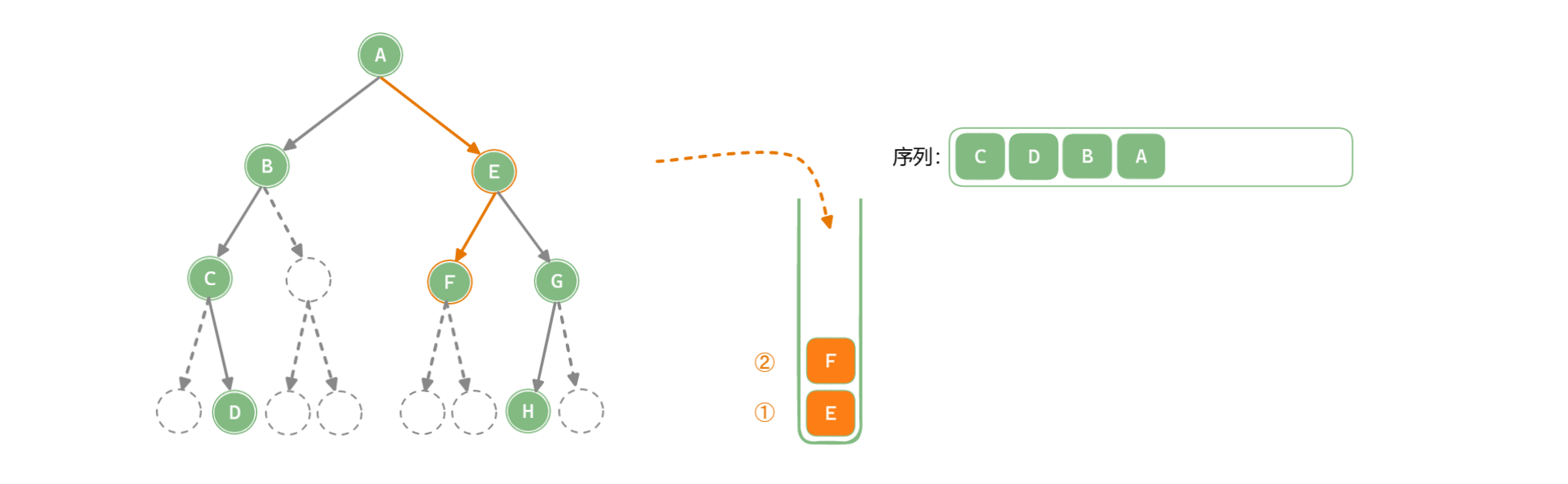
「深度优先遍历 Depth-First Traversal」使用栈作为数据存储结构,递归中使用的系统栈,系统栈会使用后自己回溯,也可以模拟栈来完成遍历。
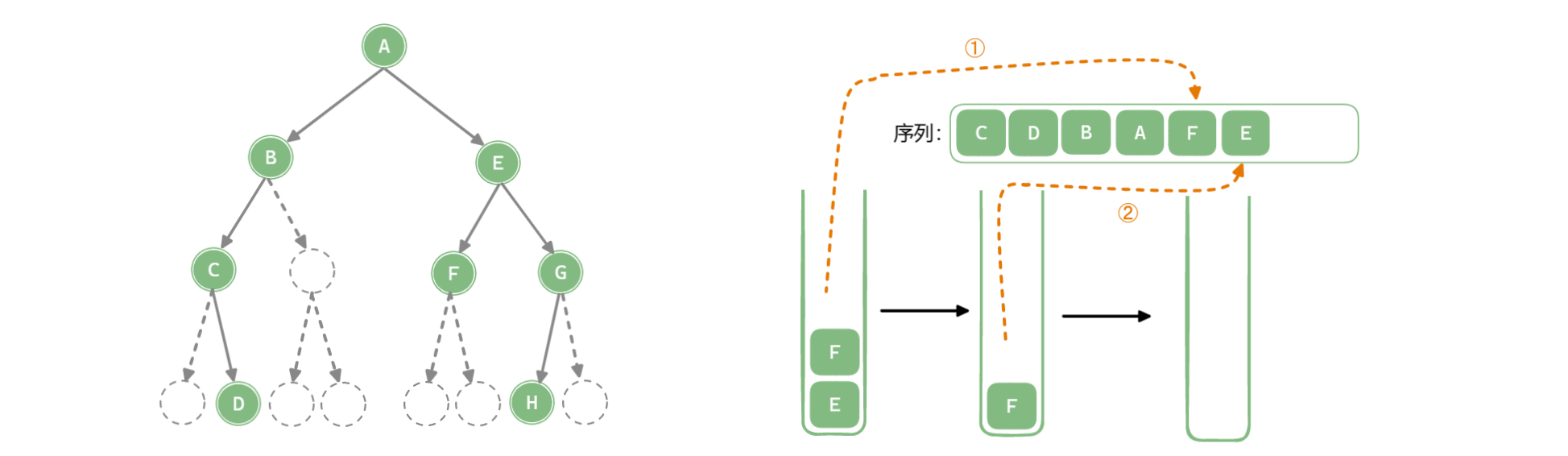
以中序遍历为例:
/**
* 前序遍历(非递归)
* @param root 根结点
* @return 前序遍历序列
*/
public List<TreeNode<T>> NoRecursivePreOrder(TreeNode<T> root) {
if (root == null) return new ArrayList<>(); // 根结点为空时返回空序列
Stack<TreeNode<T>> stack = new Stack<>(); // 初始化栈
List<TreeNode<T>> list = new ArrayList<>(); // 存储遍历序列
TreeNode<T> node = root;
while(node != null || !stack.isEmpty()) {
while (node != null) {
list.add(node); // 存储结点
stack.push(node); // 结点入栈
node = node.left; // 访问左子结点, 遍历左子树
}
if (!stack.isEmpty()) {
node = stack.pop(); // 弹出栈顶结点
node = node.right; // 访问右子结点, 遍历右子树
}
}
return list;
}
/**
* 中序遍历(非递归)
* @param root 根结点
* @return 中序遍历序列
*/
public List<TreeNode<T>> NoRecursiveInOrder(TreeNode<T> root) {
if (root == null) return new ArrayList<>(); // 根结点为空时返回空序列
Stack<TreeNode<T>> stack = new Stack<>(); // 初始化栈
List<TreeNode<T>> list = new ArrayList<>(); // 存储遍历序列
TreeNode<T> node = root;
while(node != null || !stack.isEmpty()) {
while (node != null) {
stack.push(node); // 结点入栈
node = node.left; // 访问左子结点, 遍历左子树
}
if (!stack.isEmpty()) {
node = stack.pop(); // 弹出栈顶结点
list.add(node); // 存储结点
node = node.right; // 访问右子结点, 遍历右子树
}
}
return list;
}
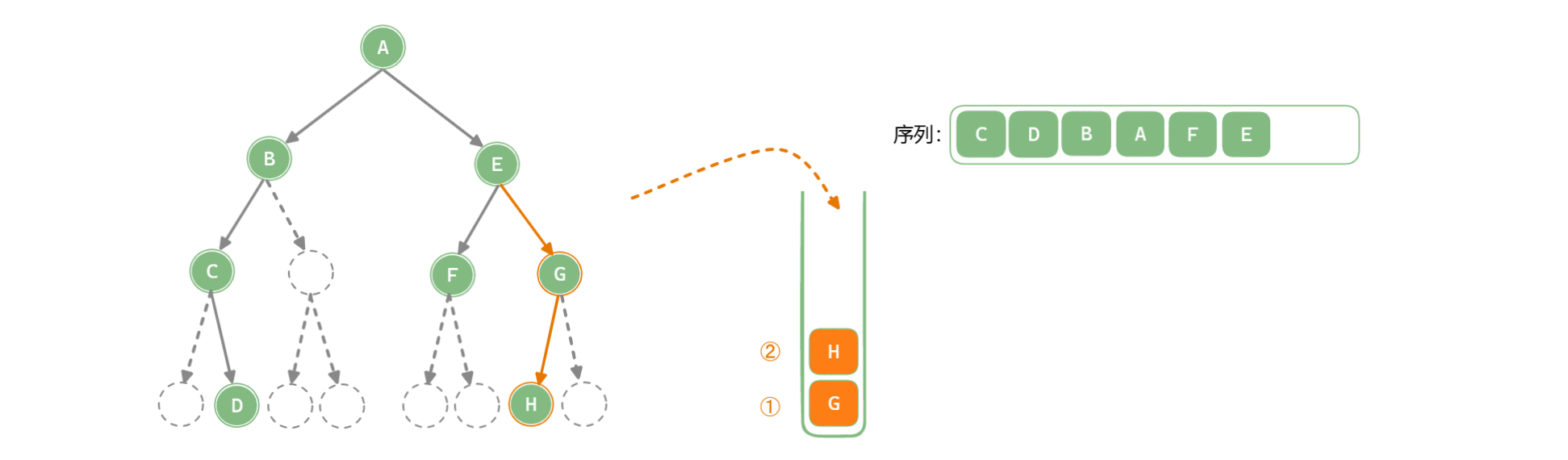
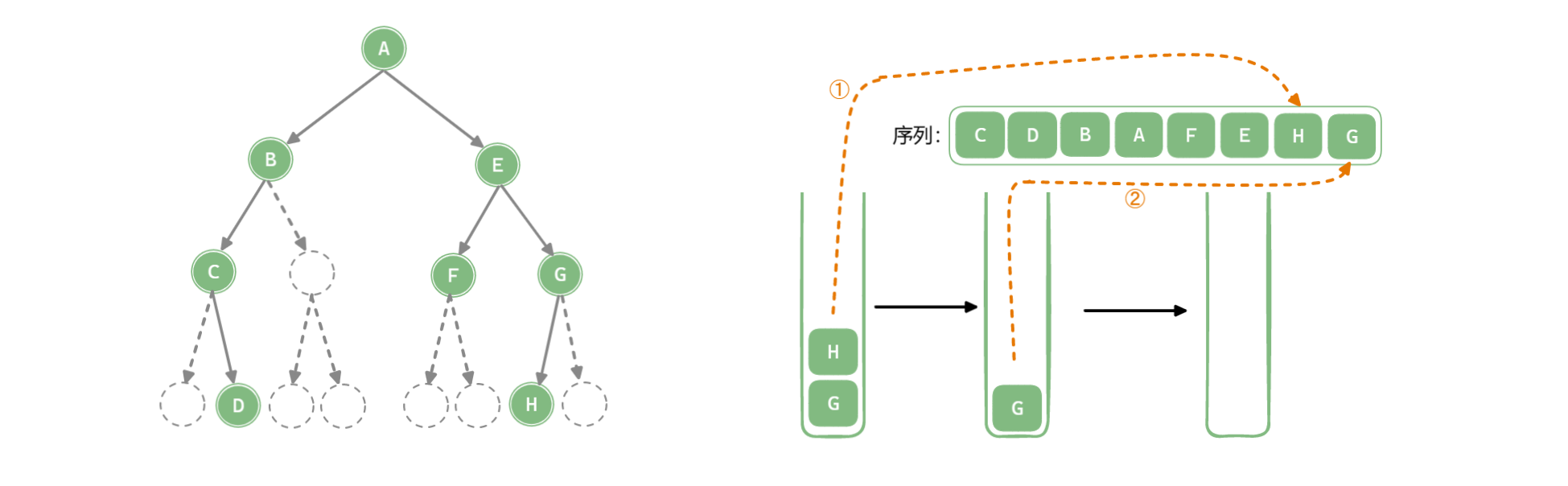
后序遍历与前序遍历、中序遍历不同,后序遍历过程中,当一个结点作为 “根结点” 时,它的左子树遍历完之后不能出栈,必须等到右子树遍历完成之后才可以出栈,所以需要对当前结点的右子树是否遍历完成做出判断。
/**
* 后序遍历(非递归)
* @param root 根结点
* @return 后序遍历序列
*/
public List<TreeNode<T>> NoRecursivePostOrder2(TreeNode<T> root) {
Stack<TreeNode<T>> stack = new Stack<>();
boolean vistited = false; // 为 false 时 ,当前结点右子树未被访问; 为 true 时, 右子树已被访问
List<TreeNode<T>> list = new ArrayList<>(); // 存储序列
while (root != null || !stack.isEmpty()) {
while (root != null && !vistited) {
stack.push(root);
root = root.left;
}
TreeNode<T> topNode = stack.peek(); // 查看栈顶结点
if (topNode.right != null && !vistited) { // 栈顶结点右子树不为空并且未被访问时
root = topNode.right; // 遍历右子树
}
else { // 栈顶结点右子树为空 或者 已被访问
TreeNode<T> node = stack.pop(); // 此时该结点可以出栈
list.add(node); // 当前结点已被访问但是右子树不为空
if (node.right != null) { // 当前结点右子树不为空时,说明还未遍历其右子树
vistited = false; // 目的是更新之前已经遍历完其他结点的右子树时的 visited = true
}
if (stack.isEmpty()) {
break;
}
root = stack.peek().right;
if (root == node) { // 如果此时栈顶的结点是当前结点作为根结点 的 右子树的根结点时
vistited = true; // 则右子树已遍历完成
}
}
}
return list;
}
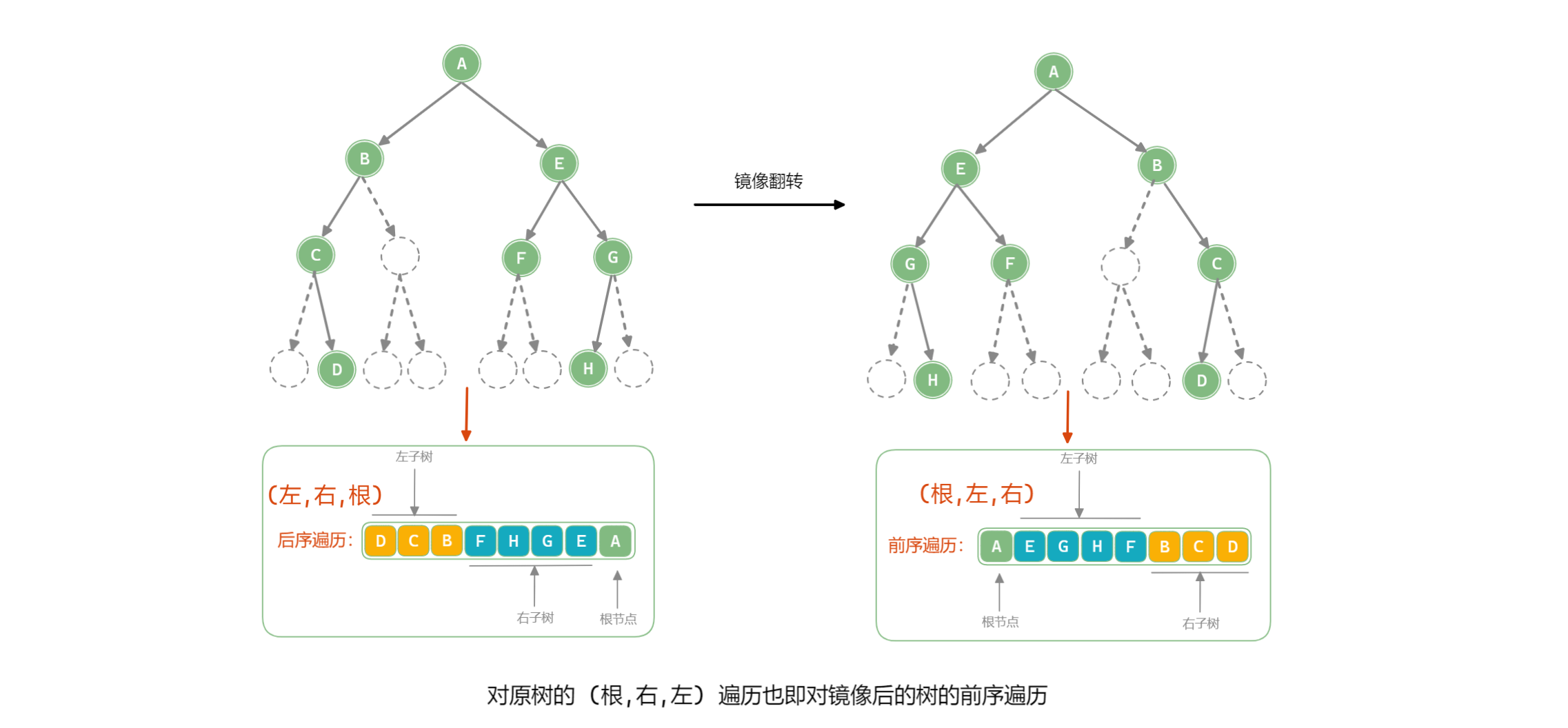
上述思路有些麻烦,原二叉树镜像之后的树的前序遍历的翻转正好是原树的后序遍历,如下图:
/**
* 后序遍历 (非递归, 镜像后树的前序遍历)
* @param root 根结点
* @return 后序遍历序列
*/
public List<TreeNode<T>> NoRecursivePostOrder(TreeNode<T> root) {
List<TreeNode<T>> list = new ArrayList<>(); // 存储序列
if (root != null) {
Stack<TreeNode<T>> stack = new Stack<>();
stack.push(root); // 根结点入栈
while (!stack.isEmpty()) {
TreeNode<T> node = stack.pop();
list.add(node);
if (node.left != null) {
stack.push(node.left); // 左子结点先入栈 (后出栈)
}
if (node.right != null) {
stack.push(node.right); // 右子结点后入栈 (先出栈)
}
}
// 上面出栈的顺序是 根 -> 右 -> 左 ,
// 然后将此反转之后就是 左 -> 右 -> 根, 正好就是后序遍历
Collections.reverse(list);
}
return list;
}
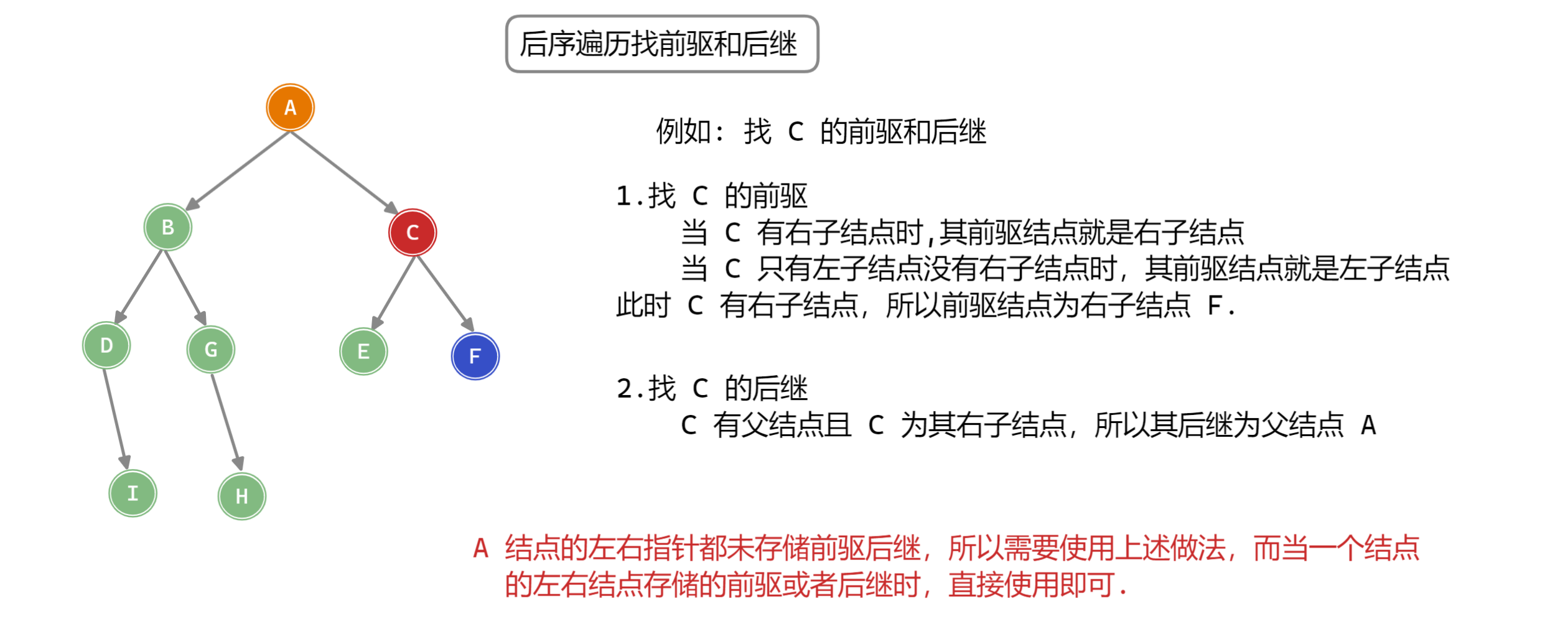
线索二叉树
「线索二叉树 Thread Binary Tree」利用二叉树中未被利用的指针表示某种遍历序列中前驱和后序信息的二叉树。
一般的链表存储二叉树时只存储结点之间的父子关系,对于 个结点的二叉树来说,每个结点都有左右两个指针,共有 个,而父子关系 (二叉树中的边) 共有 ,所以还剩 的指针没有表示任何关系 (未被利用),所以引入线索二叉树的原因是加快查找某种遍历序列下结点的前驱和后继,从而通过某种遍历顺序下结点的前驱和后继直接进行某种顺序的遍历。(若不使用线索二叉树直接存储的话,每次找一个结点的前驱或者后继的时候,都需要重新进行一次遍历,这样效率很低)
线索二叉树的结点表示信息如下:

为线索二叉树的结点增加信息如下:
// 子结点标志
enum NodeTag {
childNode, // 子结点
/**
* 前驱结点或者后继结点 <br>
* 对于左子结点来说是前驱结点 <br>
* 对于右子结点来说是后继结点
*/
orderNode,
}
public class TreeNode<T extends Comparable<T>> {
public T value; // 结点值
public TreeNode<T> left; // 左子结点
public TreeNode<T> right; // 右子结点
public NodeTag leftTag; // 左指针标识
public NodeTag rightTag; // 右指针标识
public TreeNode(T value) {
this.value = value;
// 初始化枚举的默认值
this.leftTag = NodeTag.childNode;
this.rightTag = NodeTag.childNode;
}
}
为二叉树增加一个全局前驱结点,用于线索化时处理前驱节点的后继结点
class BinaryTree<T extends Comparable<T>> {
TreeNode<T> pre; // 全局变量, 存储前驱结点, 以处理其后继结点
public BinaryTree(TreeNode<T> root) {
this.root = root;
this.pre = null; // 初始化前驱结点
}
}
中序线索二叉树
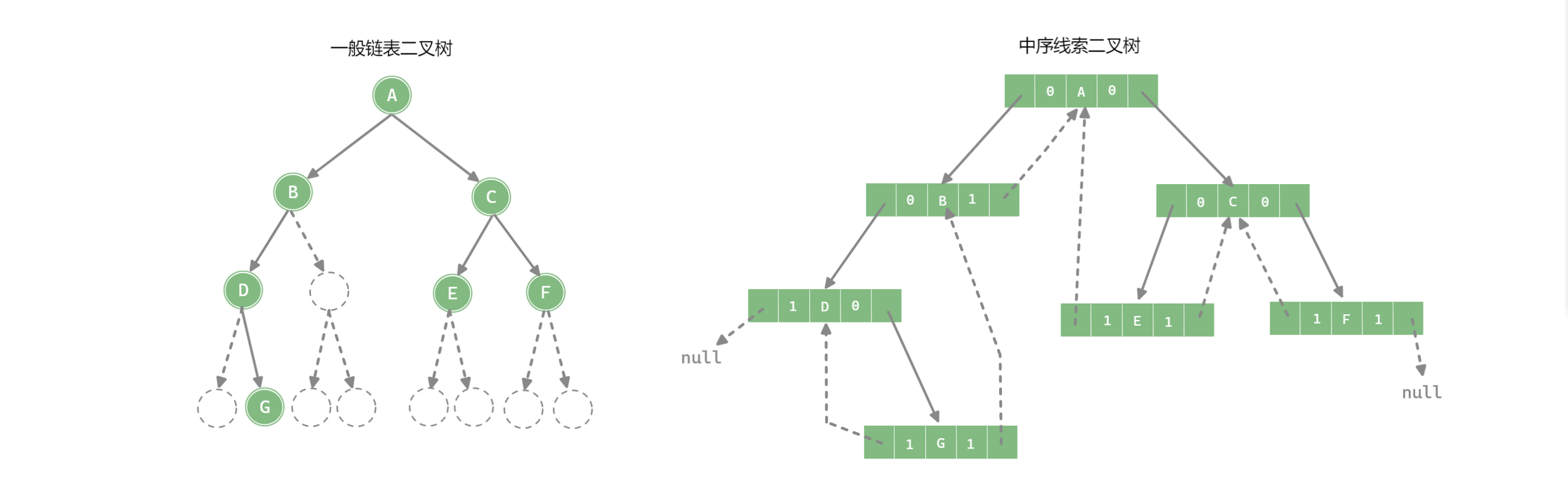
构造中序线索二叉树
/**
* 将基本二叉树改为中序线索二叉树
*/
public void CreatInOrderThread(TreeNode<T> root) {
if (root != null) inOrderThead(root);
}
/**
* 中序遍历线索二叉树 (一边遍历,一边线索化)
* @param node 结点
*/
private void inOrderThead(TreeNode<T> node) {
if (node == null) return;
inOrderThead(node.left);
if (node.left == null) { // 左子树为空, 建立前驱线索
node.left = pre;
node.leftTag = NodeTag.orderNode;
}
if (node.right == null) node.rightTag = NodeTag.orderNode; // 处理右指针
if (pre != null && pre.right == null) { // 前驱结点的右子树为空,为前驱结点建立后续线索
pre.right = node;
}
pre = node;
inOrderThead(node.right);
}
使用构造好的中序线索二叉树对二叉树进行中序遍历、找前驱、找后继

/**
* 利用中序线索化二叉树存储的前驱后继对二叉树进行中序遍历
* @param root 根结点
* @return 遍历序列
*/
public List<TreeNode<T>> inOrderTBT(TreeNode<T> root) {
List<TreeNode<T>> list = new ArrayList<>();
for (TreeNode<T> p = takeFirstIn(root); p != null ; p = nextNodeIn(p))
list.add(p);
return list;
}
/**
* 找子树中的最左下结点 (也即该子树第一个被中序遍历的点)
* @param node 子树根结点
* @return 最左下结点
*/
private TreeNode<T> takeFirstIn(TreeNode<T> node) {
// 当前结点的左子结点存储的时不是前驱结点时,继续寻找最左结点
while (node.leftTag == NodeTag.childNode) {
node = node.left;
}
return node;
}
/**
* 中序线索二叉树中结点 node 的后继结点
* @param node 结点
* @return 中序遍历下 node 的后继结点
*/
public TreeNode<T> nextNodeIn(TreeNode<T> node) {
if (node == null) return null;
// 当前右子结点存的不是后继时, 返回右子树中最左下结点(leftTag == 0,非前驱结点), 即为当前结点的后继
if (node.rightTag == NodeTag.childNode) return takeFirstIn(node.right);
// rightTag == orderNode 时,其右子结点就是其后继结点
else return node.right;
}
/**
* 中序线索二叉树中结点 node 的前驱结点
* @param node 结点
* @return 中序遍历下 node 的前驱结点
*/
public TreeNode<T> lastNodeIN(TreeNode<T> node) {
if (node == null) return null;
// 当左子结点存的不是前驱时
if (node.leftTag == NodeTag.childNode) {
// 返回左子树中最右下结点(rightTag == childNode,非后继结点),即为当前结点的前驱
while (node.rightTag == NodeTag.childNode) {
node = node.right;
}
return node;
}
// leftTag == orderNode 时,其左子结点就是其前驱结点
else return node.left;
}
前序线索二叉树
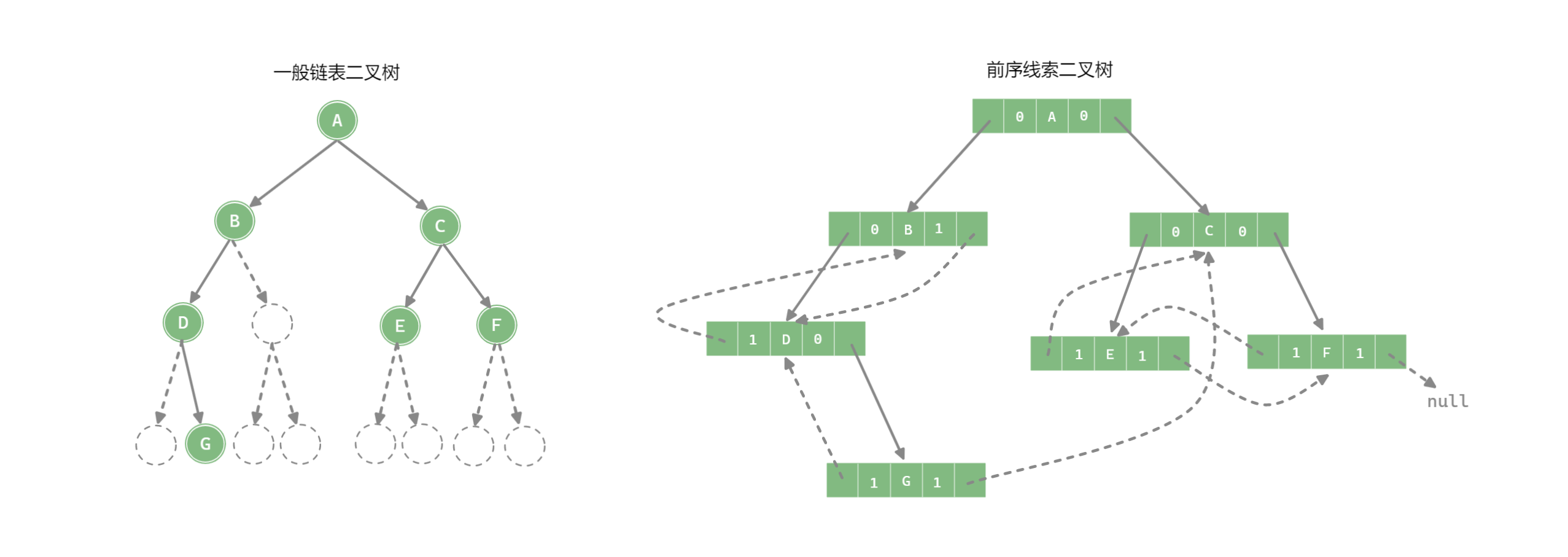
构造前序线索二叉树
/**
* 将基本二叉树改为前序序线索二叉树
* @param node 结点
*/
public void CreatPreOrderThread(TreeNode<T> node) {
if (node != null) preOrderThread(node);
}
/**
* 前序遍历线索二叉树 (一边遍历,一边线索化)
* @param node 结点
*/
private void preOrderThread(TreeNode<T> node) {
if (node == null) return;
if (node.left == null) { // 左子树为空, 建立前驱线索
node.left = pre;
node.leftTag = NodeTag.orderNode;
}
if (node.right == null) node.rightTag = NodeTag.orderNode; // 处理结点的右指针
if (pre != null && pre.right == null) { // 前驱结点的右子树为空,为前驱结点建立后续线索
pre.right = node;
}
pre = node;
// 左孩子不是前驱线索时
if (node.leftTag == NodeTag.childNode) preOrderThread(node.left);
preOrderThread(node.right);
}
注意
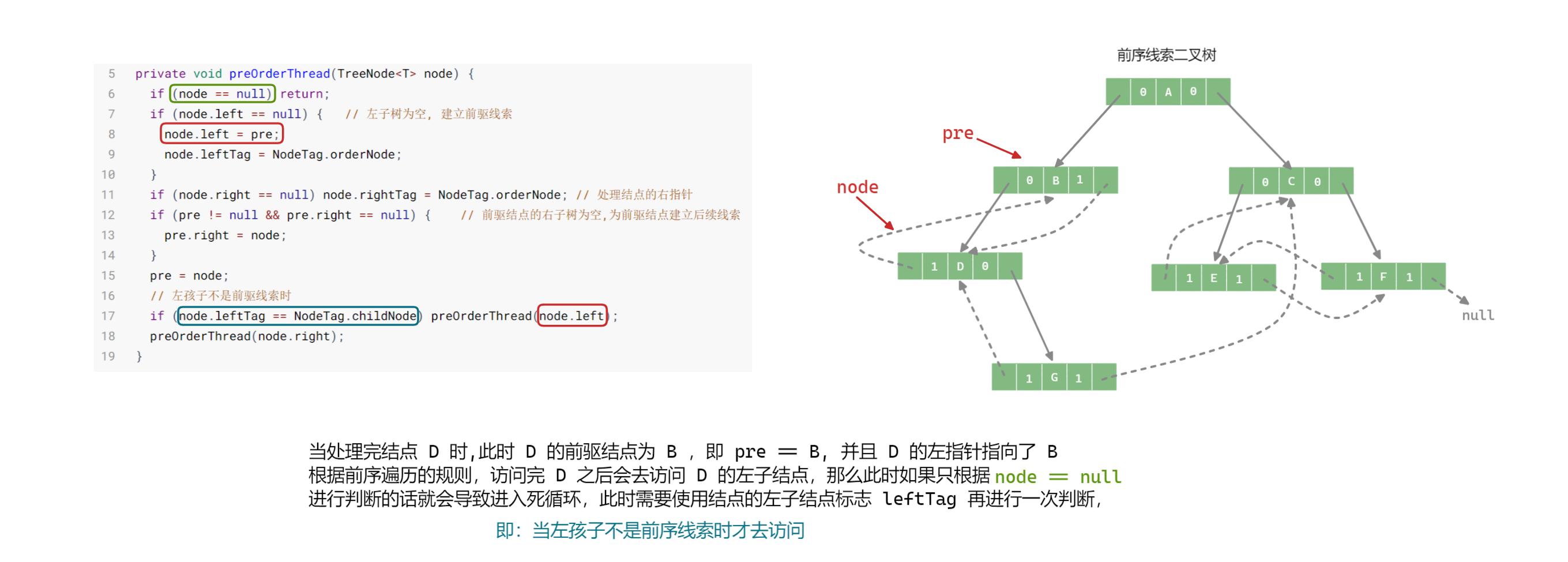
使用构造好的前序线索二叉树对二叉树进行前序遍历、找前驱、找后继
在前序线索二叉树中寻找结点的前驱时需要使用到结点的父结点,所以对结点信息进行修改,同时需要在构建二叉树时初始化每个结点的父结点
详情
public class TreeNode<T extends Comparable<T>> {
public T value; // 结点值
public int height; // 结点高度
public TreeNode<T> left; // 左子结点
public TreeNode<T> right; // 右子结点
public NodeTag leftTag; // 左指针标识
public NodeTag rightTag; // 右指针标识
public TreeNode<T> parent; // 当前结点的父结点
/**
* 从数组数据中构建二叉树
* @param arr 结点数组 (层序遍历存储的完全二叉树(空结点为 null))
* @return 链表二叉树
* @param <T> 结点对应的数据类型
*/
public static <T extends Comparable<T>> TreeNode<T> arrToTree(T[] arr) {
if (arr.length == 0)
return null;
TreeNode<T> root = new TreeNode<>(arr[0]);
Queue<TreeNode<T>> queue = new LinkedList<>() { { add(root); }};
int i = 1;
while(!queue.isEmpty()) {
TreeNode<T> node = queue.poll();
if(arr[i] != null) {
node.left = new TreeNode<>(arr[i]);
node.left.parent = node;
queue.add(node.left);
}
i++;
if(arr[i] != null) {
node.right = new TreeNode<>(arr[i]);
node.right.parent = node;
queue.add(node.right);
}
i++;
}
return root;
}
}
有了父结点就可以更加方便的寻找结点的前驱
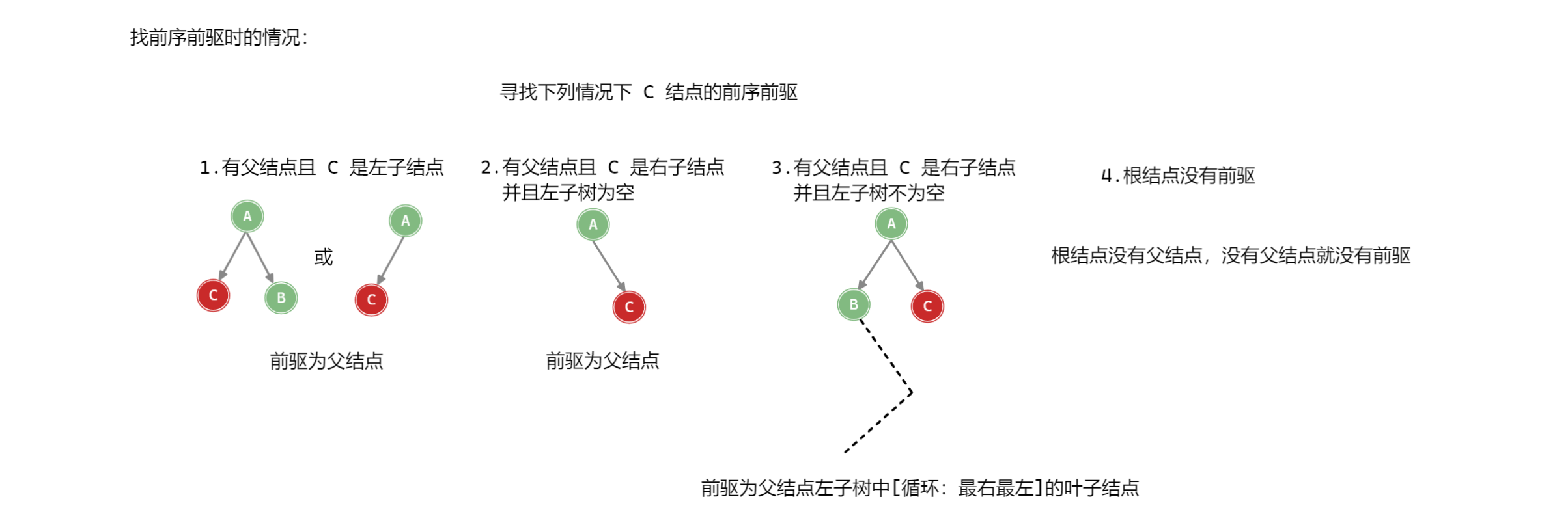

/**
* 寻找子树中最后一个被前序遍历的结点
* @param node 子树根结点
* @return 该子树中最后一个被前序遍历的结点
*/
public TreeNode<T> takeLast(TreeNode<T> node) {
while (true) {
// 寻找右子树
while (node.rightTag == NodeTag.childNode) {
node = node.right;
}
// 寻找右子树的左子树
while (node.leftTag == NodeTag.childNode) {
node = node.left;
}
// 当该结点为叶子结点时返回
if (node.leftTag == NodeTag.orderNode && node.rightTag == NodeTag.orderNode)
break;
}
return node;
}
/**
* 寻找在前序遍历下该结点的前驱结点
* @param node 结点
* @return 前序前驱结点
*/
public TreeNode<T> LastNodePre(TreeNode<T> node) {
if (node == null) return null;
// 结点的父结点非空时
TreeNode<T> parent = node.parent;
// 父结点存在时
if (parent != null) {
// 当前结点是父节点的有结点且其兄弟结点不为空
if (parent.right == node && parent.left != null)
return takeLast(parent.left);
}
return parent;
}
/**
* 寻找在前序遍历下该结点的后继结点
* @param node 结点
* @return 前序后继结点
*/
public TreeNode<T> NextNodePre(TreeNode<T> node) {
// 根左右, 若左子结点不为空, 其一定是后继
if (node.left != null && node.leftTag == NodeTag.childNode)
return node.left;
else return node.right;
}
/**
* 前序线索树下使用其存储的前驱后继进行前序遍历
* @param node 根结点
* @return 前序遍历顺序
*/
public List<TreeNode<T>> preOrderTBT(TreeNode<T> node) {
List<TreeNode<T>> list = new ArrayList<>();
// 从根结点的左子结点开始前序遍历,
for (TreeNode<T> p = LastNodePre(node.left) ; p != null ; p = NextNodePre(p)) {
list.add(p);
}
return list;
}
后序线索二叉树
构造后序线索二叉树
/**
* 后序遍历线索二叉树 (一边遍历,一边线索化)
* @param node 结点
*/
private void postOrderThread(TreeNode<T> node) {
if (node == null) return;
postOrderThread(node.left);
postOrderThread(node.right);
if (node.left == null) { // 左子树为空, 建立前驱线索
node.left = pre;
node.leftTag = NodeTag.orderNode;
}
if (node.right == null) node.rightTag = NodeTag.orderNode; // 处理结点的右指针
if (pre != null && pre.right == null) { // 前驱结点的右子树为空,为前驱结点建立后续线索
pre.right = node;
}
pre = node;
}
/**
* 将基本二叉树改为后序线索二叉树
* @param node 结点
*/
public void CreatPostOrderThread(TreeNode<T> node) {
if (node != null) {
postOrderThread(node);
}
}
使用构造好的后序线索二叉树对二叉树进行后序遍历、找前驱、找后继
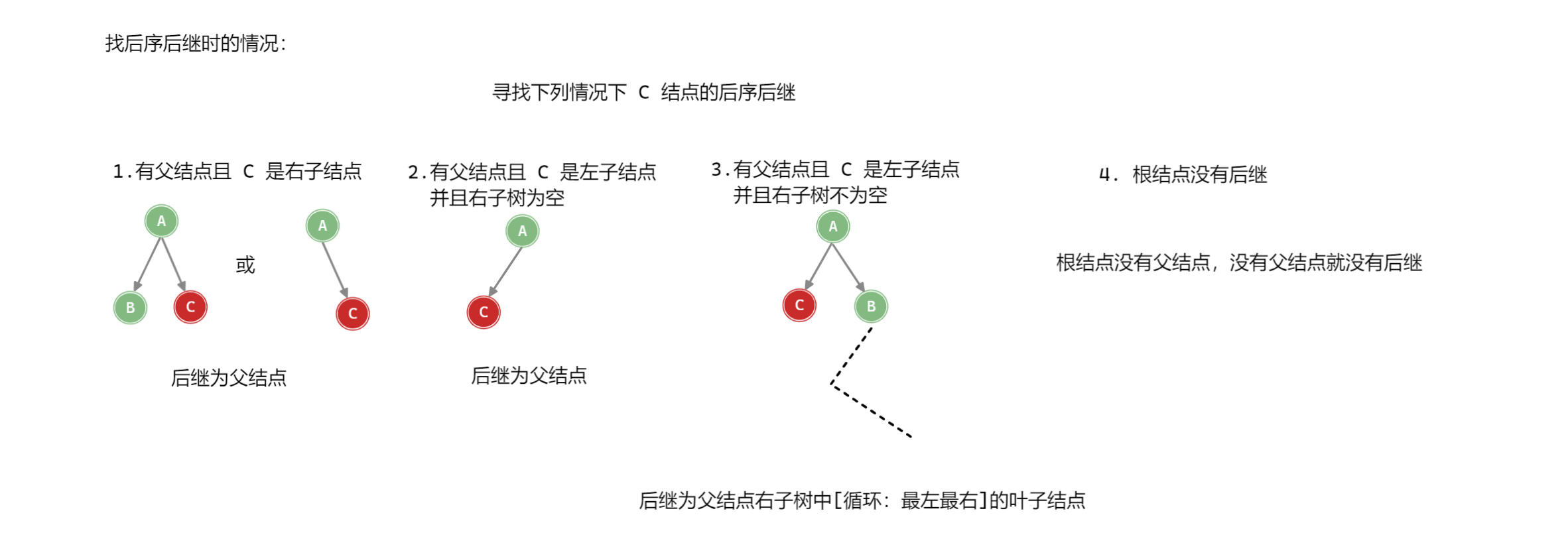
/**
* 寻找在后序遍历下该结点的前驱结点
* @param node 结点
* @return 后序前驱结点
*/
public TreeNode<T> LastNodePost(TreeNode<T> node) {
// 左右根, 若右子结点不为空, 其一定是前驱
if (node.rightTag == NodeTag.childNode && node.right != null)
return node.right;
else {
return node.left;
}
}
/**
* 寻找子树中第一个被后序遍历的结点 [循环: 最左最右]
* @param node 子树根结点
* @return 该子树中第一个被后序遍历的结点
*/
private TreeNode<T> takeFirstPost(TreeNode<T> node) {
while (true) {
// 寻找左子树
while (node.leftTag == NodeTag.childNode) {
node = node.left;
}
// 寻找左子树的右子树
while (node.rightTag == NodeTag.childNode) {
node = node.right;
}
// 当该结点为叶子结点时返回
if (node.leftTag == NodeTag.orderNode && node.rightTag == NodeTag.orderNode)
break;
}
return node;
}
/**
* 寻找在后序遍历下该结点的后继结点
* @param node 结点
* @return 后序后继结点
*/
public TreeNode<T> NextNodePost(TreeNode<T> node) {
if (node == null) return null;
// 结点的父节点非空时
TreeNode<T> parent = node.parent;
if (parent != null) {
if (parent.left == node && parent.right != null)
return takeFirstPost(parent.right);
}
return parent;
}
/**
* 后序线索树下使用其存储的前驱后继进行后序遍历
* @param node 根结点
* @return 前序遍历顺序
*/
public List<TreeNode<T>> postOrderTBT(TreeNode<T> node) {
List<TreeNode<T>> list = new ArrayList<>();
// 根结点先入序列
list.add(node);
// 从根结点开始,找前驱
for (TreeNode<T> p = LastNodePost(node) ; p != null ; p = LastNodePost(p)) {
list.add(p);
}
// 再翻转一下
Collections.reverse(list);
return list;
}






