哈夫曼树
「哈夫曼树 Huffman Tree」
「哈夫曼树」也称「最优二叉树」,在含有 个带权叶结点的二叉树中,其中带权路径长度 ( WPL ) 最小的二叉树就是哈夫曼树。
哈夫曼树相关术语
- 结点的权值 (weight):有某种现实含义的数值 (如: 表示结点的重要性)
- 结点的「带权路径长度 weighted path length」(WPL):从树的根结点到该结点的路径长度 (经过的边数) 与该结点上权值的乘积
- 树的带权路径长度:树中所有叶结点的带权路径长度之和:
其中, 为第 个叶子结点的权值, 为从根结点到第 个叶子结点的路径长度(经过的边数).
相关信息
从上图中可以看出,当叶子结点权值越大并且距离根结点越近时,可以使整颗树的 WPL 更小,这也符合哈夫曼树的定义.
计算 WPL 时可使用「小根堆(优先队列)」来实现:
use std::collections::BinaryHeap;
use std::cmp::Reverse;
/**
* v: 初始各个结点的值
* return : wpl
*/
fn cal_wpl(v: Vec<usize>) -> usize {
let mut heap = BinaryHeap::<Reverse<usize>>::new();
// 初始化小根堆
for i in v { heap.push(Reverse(i)); }
let mut wpl = 0;
// 每次选择堆中最小的两个元素
while heap.len() > 1 {
let x = heap.pop().unwrap_or(Reverse(0));
let y = heap.pop().unwrap_or(Reverse(0));
wpl = wpl + x.0 + y.0;
heap.push(Reverse(x.0 + y.0)); // 将合并后的值加入堆中
}
wpl
}
fn main() {
let v: Vec<usize> = vec![1, 3, 4, 5];
let wpl = cal_wpl(v);
println!("{}", wpl);
}
import java.util.Arrays;
import java.util.PriorityQueue;
public class Huffman {
public static void main(String[] args) {
Integer a[] = {1, 3, 4, 5};
// 定义小根堆 PriorityQueue 默认是小根堆
PriorityQueue<Integer> heap = new PriorityQueue<>();
heap.addAll(Arrays.asList(a));
Integer wpl = 0;
// 每次选择堆中最小的两个元素
while (heap.size() > 1) {
Integer x = heap.poll();
Integer y = heap.poll();
wpl += x + y;
heap.add(x + y); // 将合并后的值加入堆中
}
System.out.println(wpl);
}
}
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int cal_wpl(vector<int> a) {
// 定义小根堆
priority_queue<int, vector<int>, greater<int>> heap;
// 初始化小根堆
for(auto v: a) { heap.push(v);}
int wpl = 0;
// 每次选择堆中最小的两个元素
while ( heap.size() > 1) {
int x = heap.top();
heap.pop();
int y = heap.top();
heap.pop();
wpl += x + y;
heap.push(x + y); // 将合并后的值加入堆中
}
return wpl;
}
int main() {
vector<int> a = {1, 3, 4, 5};
int wpl = cal_wpl(a);
cout << wpl << endl;
return 0;
}
哈夫曼树的构造
给定 个权值分别为 , ,… , 的结点,构造哈夫曼树的过程如下:
- 将这 个结点分别作为 颗仅含一个结点的二叉树,构成森林 ;
- 构造一个新结点,从 中选取两颗根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和;
- 从 中删除已选择的树,同时将新得到的树加入 中;
- 重复步骤
2.3.,直至 中只剩下一颗树。
构造之后的哈夫曼树的性质:
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越长
- 哈夫曼树的结点总数为
- 哈夫曼树中不存在度为 的结点
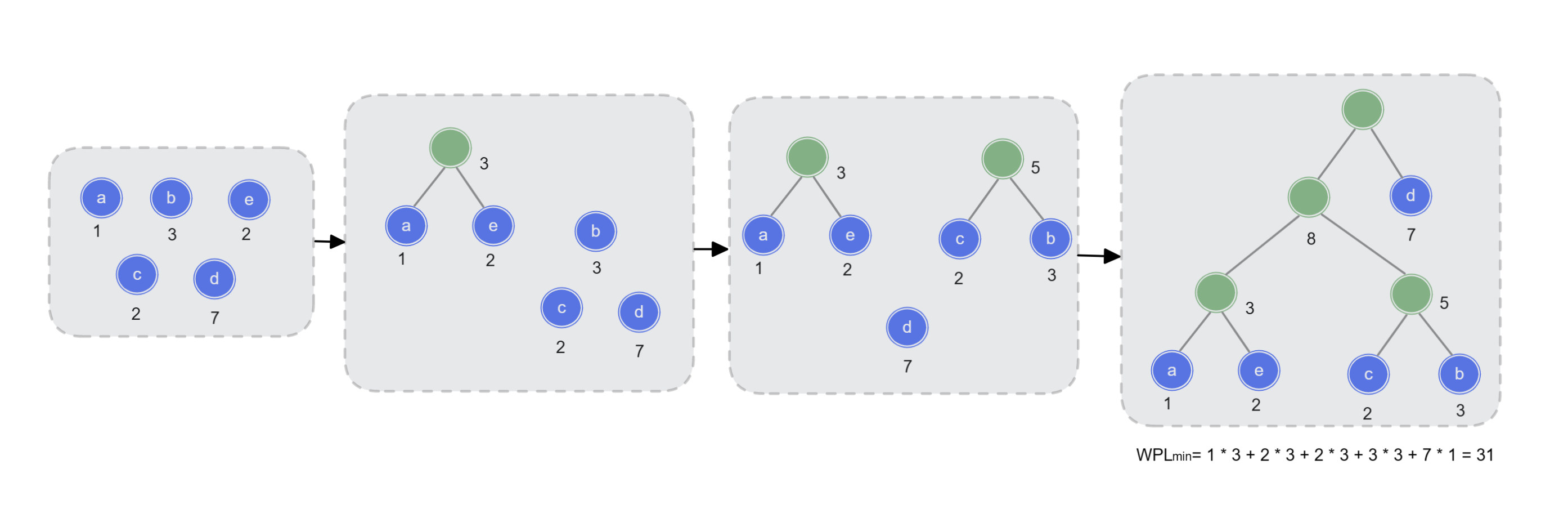
例如:使用下列结点构造哈夫曼树,结点下方为其权值
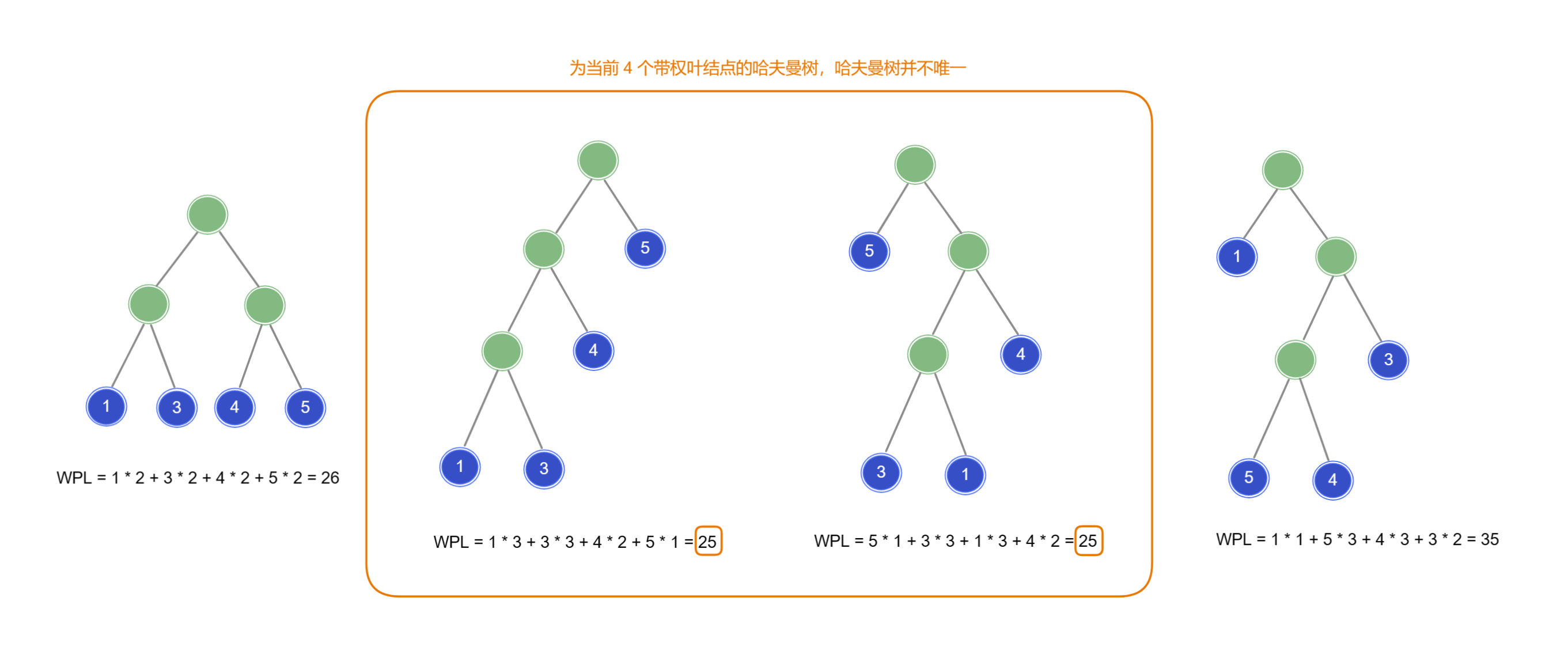
注意
构造的哈夫曼树并不唯一,只要是根据上述要求进行构造的且 WPL都是最小且一致的都是哈夫曼树.
哈夫曼树的应用
哈夫曼编码
「等长编码」是指表示字符的编码都是等长的,那么表示 个不同字符需要 位,例如:如果使用等长编码表示 ASCII 字符集,每个字符需要 位编码;
当每个字符的使用频率相等时,则「等长编码」是一种空间效率最高的编码方式,但是当频率不同时,等长编码往往不是最优选择,此时可采用「不等长编码」,将使用频率高的字符使用更少的编码表示,将使用频率低的字符使用更多的编码表示,以此来获得更好的空间效率。
注意
对于不等长编码的设计需要谨慎,因为其可能导致歧义,例如:用 0 表示 A,1 表示 B ,用 10 表示 C ,此时发来编码 1010 ,则对其的解码可以为 BABA 或者 CC ,这就产生了歧义。
「前缀编码 prefix code 」是指一组编码中任一编码都不是其他任何一个编码的前缀。 —— 这就保证了解码时不会出现歧义。
而「哈夫曼编码」就是一种「前缀编码」,其是最短的不等长编码方案。也即有最好的空间效率 (占用最少的空间)。
哈夫曼编码的构造过程
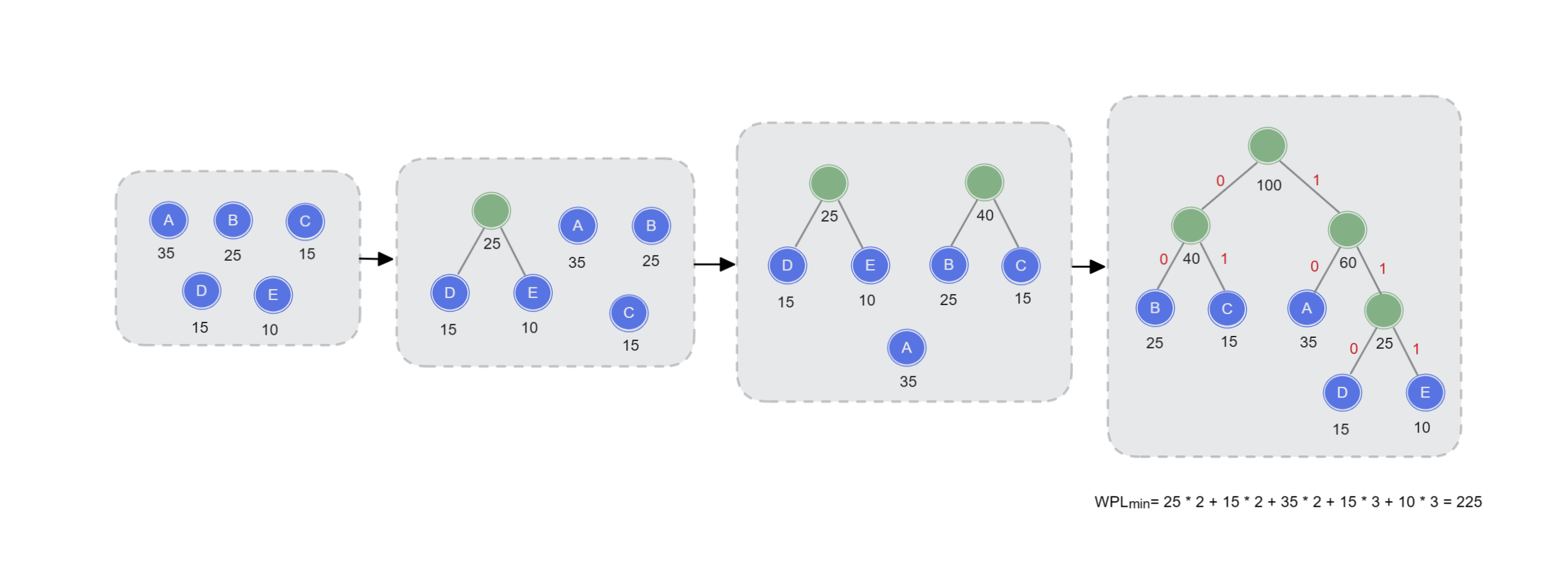
其构造过程就是构造哈夫曼树的过程,将字符出现的频率替换为权值,即可得到哈夫曼编码,如下图:
| 字符 | 频率 | 编码 |
|---|---|---|
| A | 35 | 10 |
| B | 25 | 00 |
| C | 15 | 01 |
| D | 15 | 110 |
| E | 10 | 111 |