线性代数 —— 行列式

Mr.Hdd大约 1 分钟...

行列式的定义及性质

第一种定义 (本质定义)

对于一个二阶行列式，如下：

D_2 = \left| \begin{array} {cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array} \right| = a_{11}a_{22}-a_{12}a_{21}

分别将第一行的的两个元素 $[a_{11} , a_{12}]$ 看作是一个二维向量 $\boldsymbol{α_1}$ ，同样可以将 $[a_{21},a_{22}]$ 看作是一个二维向量 $\boldsymbol{α_2}$ .

设 $\boldsymbol{α_1}$ 的长度（模）为 $l$ ， $\boldsymbol{α_2}$ 的长度（模）为 $m$ ， $\boldsymbol{α_1}$ 与 $x$ 轴正向的夹角为 $α$ ， $\boldsymbol{α_2}$ 与 $x$ 轴正向的夹角为 $β$ ，如下图所示：

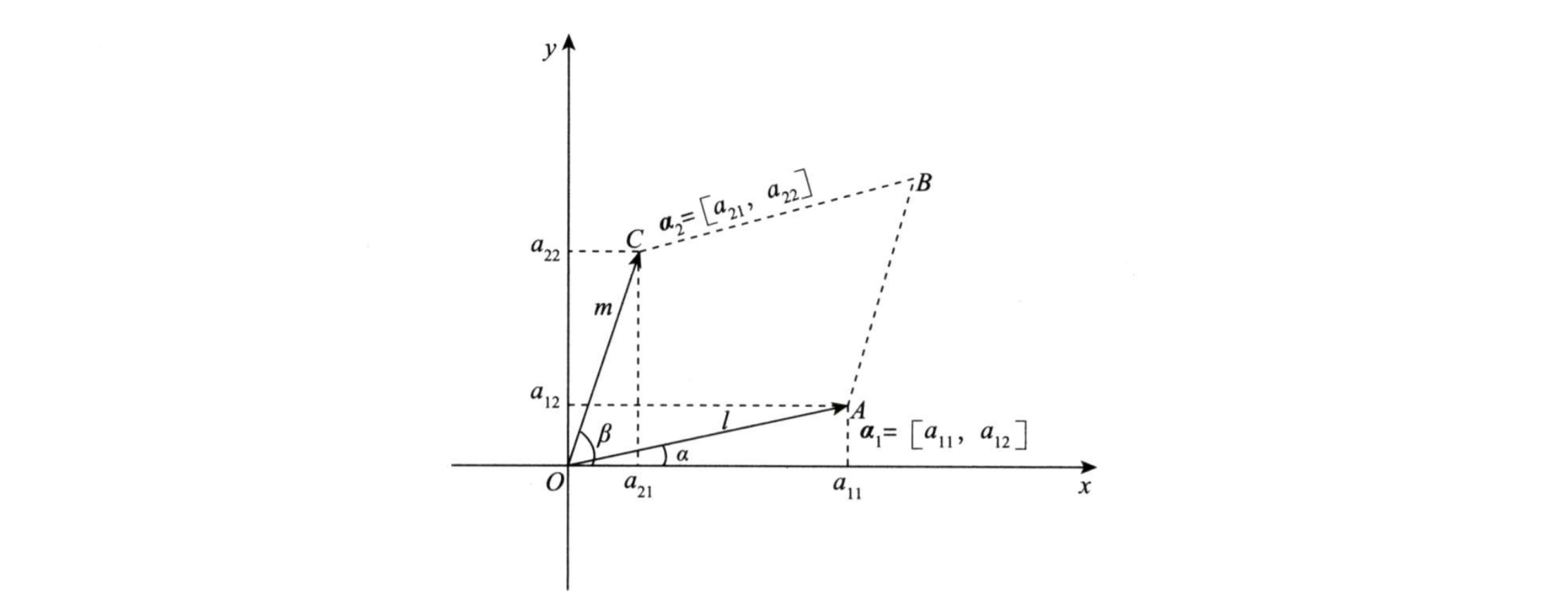
可见图中由 $α_1$ , $α_2$ 向量组成图形的面积：

\begin{aligned} S_{\square O A B C} & =l \cdot m \cdot \sin (\beta-\alpha) \\ & =l \cdot m(\sin \beta \cos \alpha-\cos \beta \sin \alpha) \\ & =l \cos \alpha \cdot m \sin \beta-l \sin \alpha \cdot m \cos \beta \\ & =a_{11} a_{22}-a_{12} a_{21}, \end{aligned}

所以有：

D_2= \left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|=a_{11} a_{22}-a_{12} a_{21}=S_{\square O A B C} .

继续推广到 $3$ 阶，那么 $3$ 阶行列式的值就等于由三维向量组成的平行六面体的体积：

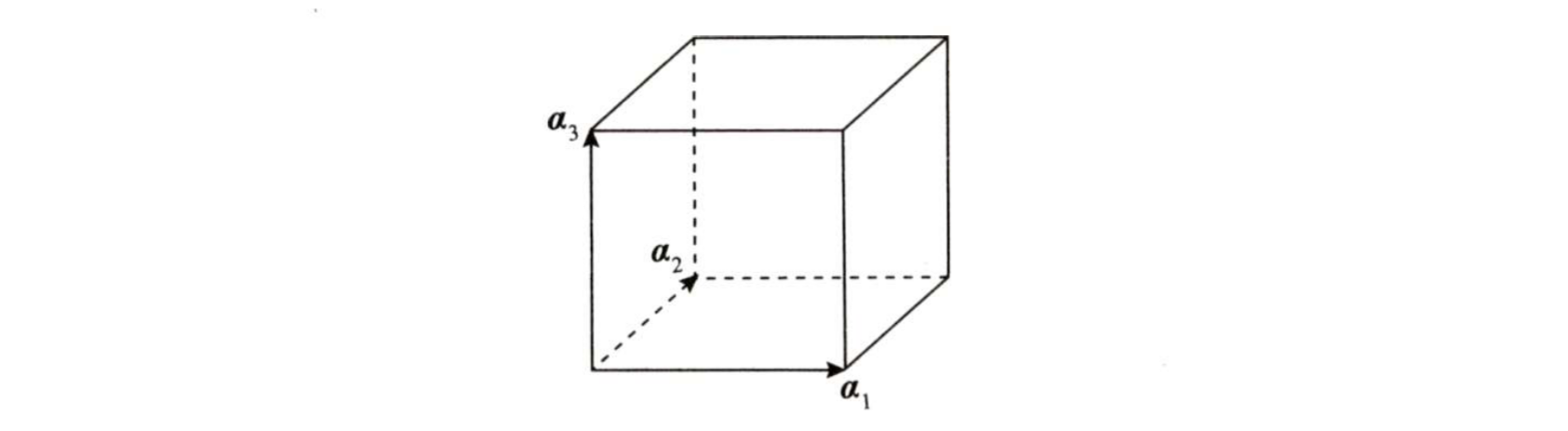
所以对于 $n$ 阶行列式的定义为：

$n$ 阶行列式是由 $n$ 个 $n$ 维向量 $\boldsymbol{\alpha}_{1}=\left[a_{11}, a_{12}, \cdots, a_{1 n}\right], \boldsymbol{\alpha}_{2}=\left[a_{21}, a_{22}, \cdots, a_{2 n}\right], \cdots, \boldsymbol{\alpha}_{n}=\left[a_{n 1}, a_{n 2}, \cdots, a_{nn}\right]$ 组成的，其 (运算规则的) 结果为以这 $n$ 个向量为邻边的 $n$ 维图形的体积。