递归

「递归 recursion」

递推与递归的宏观描述

​ 对于一个待求解的问题，当其局限于某处边界、某个小范围或者某种特殊情况下时，其答案往往是已知的。如果可以将该解答的应用场景扩大到原问题的状态空间，并且扩展过程的每个步骤具有相似性，就可以考虑使用递归或者递推来解决该问题。

• 由 “问题边界” 向 “原问题” 正向推导的过程就是递推；

• 以 “原问题” 作为起点尝试寻找将状态空间缩小到已知的 “问题边界” 的路线，再通过该路线反向回溯的遍历方式就是递归。【反向推导，再回溯到原问题】

当使用递推和递归要求 “原问题” 与 “问题边界” 之间的每个变换步骤具有相似性，

汉诺塔问题

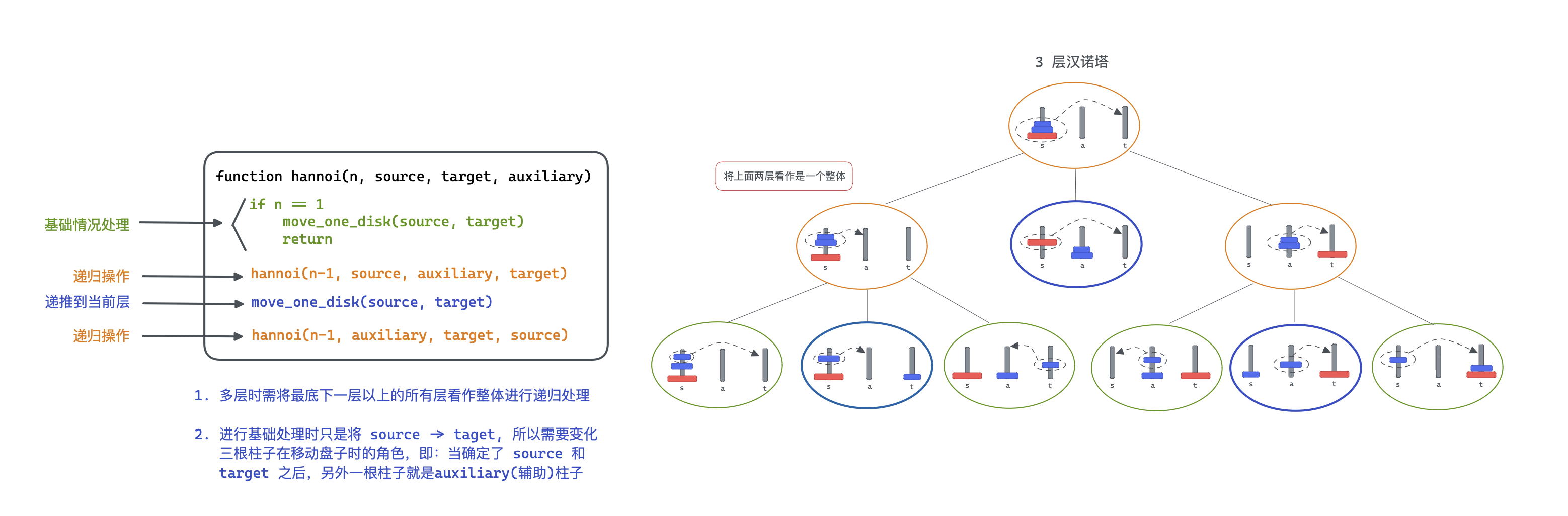
对于整个问题而言，整体解决步骤可以分为三步：

1. 将前 $n-1$ 个盘子从 $source$ 柱移动到 $axuiliary$ 柱；
2. 再将第 $n$ 个盘子从 $source$ 柱移动到 $target$ 柱；
3. 最后再将第一步中移动到 $auxiliary$ 柱的前 $n-1$ 个盘子移动到 $target$ 柱。

即得到 挪动的最小次数 如下列数学表达式：

$$f[n] = 2 \times f[n-1] + 1$$

解决汉诺塔问题的递归代码:

fn hannoi(n: usize, source: char, target: char, auxiliary : char, ans:&mut usize) {
  if n == 1 {
    *ans += 1;
    println!("{} -> {}", source, target);
    return;
  }
  hannoi(n - 1, source, auxiliary, target, ans);
  *ans += 1;
  println!("{} -> {}", source, target);
  hannoi(n - 1, auxiliary, target, source, ans);
}

fn _hannoi(n: usize, source: char, target: char, auxiliary : char, ans:&mut usize) {
  if n > 0 {
    hannoi(n - 1, source, auxiliary, target, ans);
    *ans += 1;
    println!("{} -> {}", source, target);
    hannoi(n - 1, auxiliary, target, source, ans);
  }
}
fn main() {
  let mut ans = 0;
  _hannoi(3, 'S', 'T', 'A', &mut ans);
  println!("{}", ans);
}